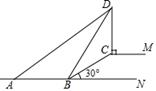
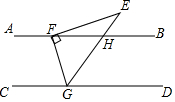
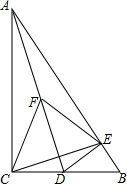
 B .
B .  C .
C .  D .
D . 
![]()



90,74,88,65,98,75,81,42,85,70,55,80,95,88,72,88,60,56,76,66,78,72,82,63,100.
| 等级 | | | | |
| 人数 | | | 8 | |
|
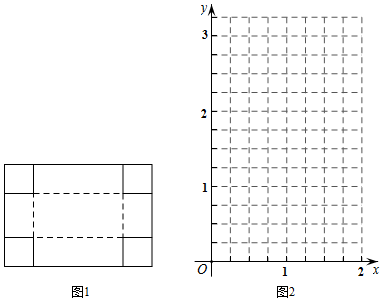
x/dm |
… |
| | | | | | | 1 | | | … |
| y/dm3 | … | 1.3 | 2.2 | 2.7 | 3.0 | 2.8 | 2.5 | 1.5 | 0.9 | … |
(注:补全表格,保留1位小数点)