希腊人常用小石子在沙滩上摆成各种性状来研究数，例如：
他们研究过图1中的1，3，6，10，…，由于这些数能够表示成三角形，将其称为三角形数；类似地，称图2中的1，4，9，16…这样的数成为正方形数。下列数中既是三角形数又是正方形数的是（ ）
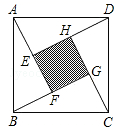
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）。小亮同学随机地在大正方形及其内部区域投针，若直角三角形的两条直角边的长分别是2和1，则针扎到小正方形（阴影）区域的概率是（ ）
B . 
C . 
D . 
求代数式的值：若a、b互为相反数，c、d互为倒数， x 等于4．求代数式 
的值．
为等边三角形．
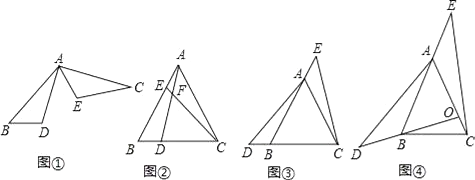
问题情境：如图①，在△ABD与△CAE中，BD=AE ， ∠DBA=∠EAC ， AB=AC ， 易证：△ABD≌△CAE ． （不需要证明）
特例探究：如图②，在等边△ABC中，点D、E分别在边BC、AB上，且BD=AE ， AD与CE交于点F ． 求证：△ABD≌△CAE ．
归纳证明：如图③，在等边△ABC中，点D、E分别在边CB、BA的延长线上，且BD=AE ． △ABD与△CAE是否全等？如果全等，请证明；如果不全等，请说明理由．
拓展应用：如图④，在等腰三角形中，AB=AC ， 点O是AB边的垂直平分线与AC的交点，点D、E分别在OB、BA的延长线上．若BD=AE ， ∠BAC=50°，∠AEC=32°，求∠BAD的度数．
， 
，顺次连接 
，得到 
为等边三角形．求证：