如图所示质量相同的三个小球A、B、C悬挂于天花板上,处于静止状态,弹簧轻质,轻质细绳不可伸缩,剪断A、B间细绳的瞬间,A、B、C三者的加速度分别为a1、a2、a3 , 则( )
![]()

如图所示,将两相同的木块a、b置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a、b均静止.弹簧处于伸长状态,两细绳均有拉力,a所受摩擦力Ffa≠0,b所受摩擦力Ffb=0,现将右侧细绳剪断,则剪断瞬间( )

如图所示,一水平方向足够长的传送带以恒定的速度v1沿顺时针方向运动,一物体以水平速度v2从右端滑上传送带后,经过一段时间又返回光滑水平面,此时速率为 v2′,则下列说法正确的是( )


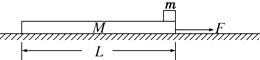
在砝码盘中每次增加10g砝码,弹簧长度依次记为L1至L6 , 数据如下表.
代表符号 | L0 | Lx | L1 | L2 | L3 | L4 | L5 | L6 |
数值(cm) | 25.35 | 27.35 | 29.35 | 31.30 | 33.4 | 35.35 | 37.40 | 39.30 |
如图是该同学根据表中数据作的图,纵轴是砝码的质量,横轴是弹簧长度与的差值(填“L0”或“Lx”).
某物理课外小组利用图(a)中的装置探究物体加速度与其所受合外力之间的关系.图中,置于实验台上的长木板水平放置,其右端固定一轻滑轮;轻绳跨过滑轮,一端与放在木板上的小滑车相连,另一端可悬挂钩码.本实验中可用的钩码共有N=5个,每个质量均为0.010kg.实验步骤如下:
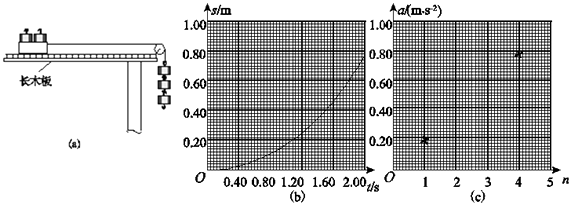
⑴将5个钩码全部放入小车中,在长木板左下方垫上适当厚度的小物块,使小车(和钩码)可以在木板上匀速下滑.
⑵将n(依次取n=1,2,3,4,5)个钩码挂在轻绳右端,其余N﹣n个钩码仍留在小车内;用手按住小车并使轻绳与木板平行.释放小车,同时用传感器记录小车在时刻t相对于其起始位置的位移s,绘制s﹣t图象,经数据处理后可得到相应的加速度a.
⑶对应于不同的n的a值见表.n=2时的s﹣t图象如图(b)所示:由图(b)求出此时小车的加速度(保留2位有效数字),将结果填入表.
n | 1 | 2 | 3 | 4 | 5 |
a(m/s2) | 0.20 | 0.58 | 0.78 | 1.00 |
⑷利用表中的数据在图(c)中补齐数据点,并作出a﹣n图象.从图象可以看出:当物体质量一定时,物体的加速度与其所受的合外力成正比.
⑸利用a﹣n图象求得小车(空载)的质量为kg(保留2位有效数字,g=9.8m/s2).
⑹若以“保持木板水平”来代替步骤(1),下列说法正确的是(填入正确选项前的标号)
A.a﹣n图线不再是直线
B.a﹣n图线仍是直线,但该直线不过原点
C.a﹣n图线仍是直线,但该直线的斜率变大.
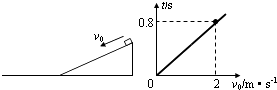
用同种材料制成倾角30°的斜面和长水平面,斜面长2.4m且固定,一小物块从斜面顶端以沿斜面向下的初速度v0开始自由下滑,当v0=2m/s时,经过0.8s后小物块停在斜面上某处.多次改变v0的大小,记录下小物块从开始运动到最终停下的时间t,作出t﹣v0图象,如图所示,求:
甲、乙两车在平直公路上比赛,某一时刻,乙车在甲车前方L1=11m处,乙车速度v乙=60m/s,甲车速度v甲=50m/s,此时乙车离终点线尚有L2=600m,如图所示.若甲车做匀加速运动,加速度a=2m/s2 , 乙车速度不变,不计车长.

如图所示一根劲度系数k=200N/m的轻质弹簧拉着质量为m=0.2kg的物体从静止开始沿倾角为θ=37°的斜面匀加速上升,此时弹簧伸长量x=0.9cm,在t=1.0s内物体前进了s=0.5m.求: 
质量为m=1.0kg的小滑块(可视为质点)放在质量为M=3.0kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长L=1.0m.开始时两者都处于静止状态,现对木板施加水平向右的恒力F=12N,如图所示,经一段时间后撤去F.为使小滑块不掉下木板,试求:用水平恒力F作用的最长时间.(g取10m/s2)