人教版数学八年级上册第14章 14.2.1平方差公式同步练...

更新时间：2017-08-24 浏览次数：1234 类型：同步测试

一、单选题

1. (2016八上·道真期末) 下列运用平方差公式计算，错误的是（）

A . （a+b）（a﹣b）=a²﹣b² B . （x+1）（x﹣1）=x²﹣1 C . （2x+1）（2x﹣1）=2x²﹣1 D . （﹣3x+2）（﹣3x﹣2）=9x²﹣4

答案解析收藏纠错 + 选题
2. (2024·从江模拟) 如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形．（a＞0）剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙）则矩形的面积为（）

A . （2a²+5a）cm² B . （3a+15）cm² C . （6a+9）cm² D . （6a+15）cm²

答案解析收藏纠错 + 选题
3. (2017·龙岩模拟) 下列计算正确的是（）

A . （x+y）²=x²+y² B . （x﹣y）²=x²﹣2xy﹣y² C . （x+1）（x﹣1）=x²﹣1 D . （x﹣1）²=x²﹣1

答案解析收藏纠错 + 选题
4. (2016八上·路北期中) 若|x+y﹣5|+（x﹣y﹣3）²=0，则x²﹣y²的结果是（）

A . 2 B . 8 C . 15 D . 16

答案解析收藏纠错 + 选题
5. (2016八上·路北期中) 化简（m²+1）（m+1）（m﹣1）﹣（m⁴+1）的值是（）

A . ﹣2m² B . 0 C . ﹣1 D . ﹣2

答案解析收藏纠错 + 选题
6. (2016八上·唐山开学考) 下列各式能用平方差公式计算的是（　　）

A . （﹣3a﹣b）（﹣3a+b） B . （3a+b）（a﹣b） C . （3a+b）（﹣3a﹣b） D . （﹣3a+b）（3a﹣b）

答案解析收藏纠错 + 选题
7.
在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（　　）

A . （a+b）²=a²+2ab+b² B . （a﹣b）²=a²﹣2ab+b² C . a²﹣b²=（a+b）（a﹣b） D . （a+2b）（a﹣b）=a²+ab﹣2b²

答案解析收藏纠错 + 选题
8. 下列变形正确的是（）

A . （﹣3a³）²=﹣9a⁵ B . 2x²y﹣2xy²=0 C . ﹣ $\text{[math]}$ ÷2ab=﹣ $\text{[math]}$ D . （2x+y）（x﹣2y）=2x²﹣2y²

答案解析收藏纠错 + 选题
9. (2017八上·上杭期末) 计算（a﹣2）（﹣a﹣2）的结果正确的是（）

A . a²﹣4 B . a²﹣4a+4 C . 4﹣a² D . 2﹣a²

答案解析收藏纠错 + 选题
10. 下列各式正确的是（）

A . （a+b）²=a²+b² B . （x+6）（x﹣6）=x²﹣6 C . （x+2）²=x²+2x+4 D . （x﹣y）²=（y﹣x）²

答案解析收藏纠错 + 选题
11. 下列计算正确的是（）

A . （2x﹣3）²=4x²+12x﹣9 B . （4x+1）²=16x²+8x+1 C . （a+b）（a﹣b）=a²+b² D . （2m+3）（2m﹣3）=4m²﹣3

答案解析收藏纠错 + 选题
12. (2017八下·临泽期末) 下列多项式中，可以用平方差公式分解因式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2024八下·拜城期中) 计算：（ $\text{[math]}$ +1）（ $\text{[math]}$ ﹣1）=．

答案解析收藏纠错 + 选题
14. (2019七下·来宾期末) 若a²﹣b²= $\text{[math]}$ ，a﹣b= $\text{[math]}$ ，则a+b的值为．

答案解析收藏纠错 + 选题
15. (2021八上·抚远期末)
如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式　．

答案解析收藏纠错 + 选题
16. (2017八上·顺庆期末) 如图，边长为m+4的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形，若拼成的矩形一边长为4，则另一边长为．

答案解析收藏纠错 + 选题

三、计算题

17. (2017八上·建昌期末) 化简：（x+y）（x﹣y）﹣（2x﹣y）（x+3y）

答案解析收藏纠错 + 选题
18. (2017八上·无锡开学考) 计算
1. （1）（π﹣2013）⁰﹣（ $\text{[math]}$ ）^﹣²+|﹣4|
2. （2） 4（a+2）（a+1）﹣7（a+3）（a﹣3）
答案解析收藏纠错 + 选题

四、综合题

19. 化简：
1. （1） ﹣（a²﹣b）²+（2a+b）（﹣2a+b）；
2. （2） $\text{[math]}$ ÷（m﹣1﹣ $\text{[math]}$ ）．
答案解析收藏纠错 + 选题
20. (2017八上·海勃湾期末) 从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．
1. （1）上述操作能验证的等式是（填A或B）
  
  A . a²﹣2ab+b²=（a﹣b）² B . a²﹣b²=（a+b）（a﹣b）
2. （2）应用你从（1）中选出的等式，计算：
  （1﹣ $\text{[math]}$ ）（1﹣ $\text{[math]}$ ）（1﹣ $\text{[math]}$ ）…（1﹣ $\text{[math]}$ ）（1﹣ $\text{[math]}$ ）．
答案解析收藏纠错 + 选题
21. 如果一个自然数能表示为两个自然数的平方差，那么称这个自然数为智慧数，例如：
16=5²﹣3² ， 16就是一个智慧数，小明和小王对自然数中的智慧数进行了如下的探索：
小明的方法是一个一个找出来的：
0=0²﹣0² ， 1=1²﹣0² ， 3=2²﹣1² ，
4=2²﹣0² ， 5=3²﹣2² ， 7=4²﹣3² ，
8=3²﹣1² ， 9=5²﹣4² ， 11=6²﹣5² ， …
小王认为小明的方法太麻烦，他想到：
设k是自然数，由于（k+1）²﹣k²=（k+1+k）（k+1﹣k）=2k+1．
所以，自然数中所有奇数都是智慧数．
问题：
1. （1）根据上述方法，自然数中第12个智慧数是；
2. （2）他们发现0，4，8是智慧数，由此猜测4k（k≥3且k为正整数）都是智慧数，请你参考小王的办法证明4k（k≥3且k为正整数）都是智慧数．
3. （3）他们还发现2，6，10都不是智慧数，由此猜测4k+2（k为自然数）都不是智慧数，请利用所学的知识判断26是否是智慧数，并说明理由．
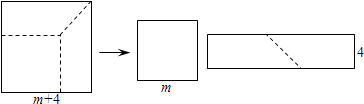
答案解析收藏纠错 + 选题