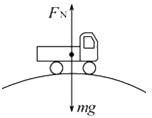
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送人同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( )

如图所示,B和C是一组塔轮,即B和C半径不同,但固定在同一转动轴上,其半径之比为RB:RC=3:2,A轮的半径大小与C轮相同,它与B轮紧靠在一起,当A轮绕过其中心的竖直轴转动时,由于摩擦作用,B轮也随之无滑动地转动起来.a、b、c分别为三轮边缘的三个点,则a、b、c三点在运动过程中的( )

在“验证动量守恒定律”的实验中,气垫导轨上放置着带有遮光板的滑块A、B,测得的质量分别为m1和m2 , 遮光板的宽度相同.实验中,用细线将两个滑块拉近使弹簧压缩,然后烧断细线,弹簧落下,两个滑块弹开,测得它们通过光电门的速率分别为υ1、υ2 . 用测量的物理量表示动量守恒应满足的关系式;本实验选用气垫导轨根本目的是.
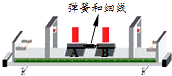
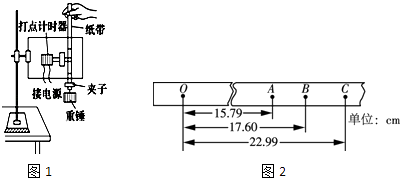
图1是“验证机械能守恒定律”的实验装置示意图,以下列出了一些实验步骤:
A.用天平测出重物和夹子的质量
B.把打点计时器用铁夹固定放到桌边的铁架台上,使两个限位孔在同一竖直面内
C.把打点计时器接在交流电源上,电源开关处于断开状态
D.将纸带穿过打点计时器的限位孔,上端用手提着,下端夹上系住重物的夹子,让重物靠近打点计时器,处于静止状态
E.接通电源,待计时器打点稳定后释放纸带,之后再断开电源
F.用秒表测出重物下落的时间
G.更换纸带,重新进行两次实验
图2为实验中打出的一条纸带,O为打出的第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出),打点计时器每隔0.02s打一个点.若重物的质量为0.5kg,当地重力加速度取g=9.8m/s2 , 由图乙所给的数据可算出(结果保留两位有效数字):
①从O点下落到B点的过程中,重力势能的减少量为J.
②打B点时重物的动能为J.
水平面上静止放置一质量为m=0.2kg的物块,固定在同一水平面上的小型电动机通过水平细线牵引物块,使物块由静止开始做匀加速直线运动,2秒末到达额定功率,其v﹣t图线如图所示,物块与水平面间的动摩擦因数为μ=0.1,g=10m/s2 , 电动机与物块间的距离足够远,求:

如图所示,在竖直平面内有轨道ABC,其中AB段为水平直轨道,与质量m=0.5kg的小物块(可视为质点)之间的动摩擦因数μ=0.2,BC段为光滑半圆形轨道,轨道半径R=2m,轨道AB与BC在B点相切.小物块在水平拉力F=3N的作用下从A点由静止开始做匀加速直线运动,到达圆弧轨道的最低点B时撤去拉力,此时速度vB=10m/s.取g=10m/s2 , 则:

如图,有一质量为M=2kg的平板车静止在光滑的水平地面上,现有质量均为m=1kg的小物块A和B(均可视为质点),由车上P处开始,A以初速度v1=2m/s向左运动,B同时以v2=4m/s向右运动,最终A、B两物块恰好停在小车两端没有脱离小车,两物块与小车间的动摩擦因数都为μ=0.1,取g=10m/s2 , 求:
