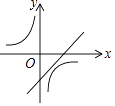
 B .
B . 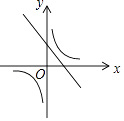 C .
C . 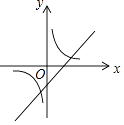 D .
D . 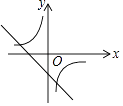
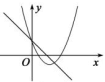 B .
B . 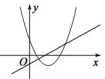 C .
C . 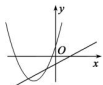 D .
D . 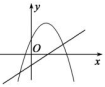
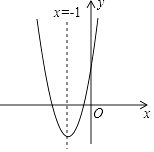
①b2=4ac;②abc>0;③a>c;④4a﹣2b+c>0,其中正确的个数有( )
|
销售第x天 |
第1天 |
第2天 |
第3天 |
第4天 |
… |
第30天 |
|
销售单价m(元/件) |
49 |
48 |
47 |
46 |
… |
20 |
|
日销售量n(件) |
45 |
50 |
55 |
60 |
… |
190 |