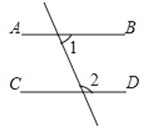
 B .
B .  C .
C .  D .
D . 
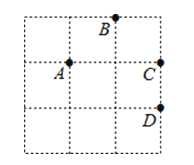
如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
定义:长宽比为:1(n为正整数)的矩形称为
矩形.
下面,我们通过折叠的方式折出一个矩形,如图①所示.


操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH.
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF.
则四边形BCEF为矩形.
证明:设正方形ABCD的边长为1,则BD==
.
由折叠性质可知BG=BC=1,∠AFE=∠BFE=90°,则四边形BCEF为矩形.
∴∠A=∠BFE.
∴EF∥AD.
∴=
, 即
=
.
∴BF= .
∴BC:BF=1:=
:1.
∴四边形BCEF为矩形.
阅读以上内容,回答下列问题: