 B .
B .  C .
C .  D .
D . 
 B .
B . 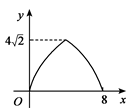 C .
C . 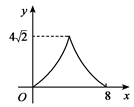 D .
D . 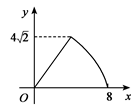


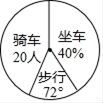
治理杨絮一一您选哪一项?(单选)
A.减少杨树新增面积,控制杨树每年的栽种量
B.调整树种结构,逐渐更换现有杨树
C.选育无絮杨品种,并推广种植
D.对雌性杨树注射生物干扰素,避免产生飞絮
E.其他
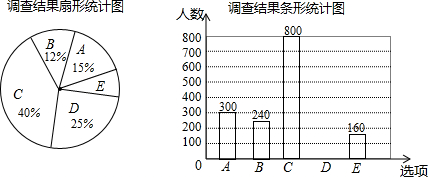
根据以上统计图,解答下列问题:
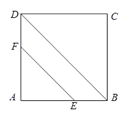
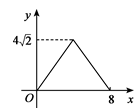
方案甲中AD的长不超过墙长;方案乙中AD的长大于墙长.
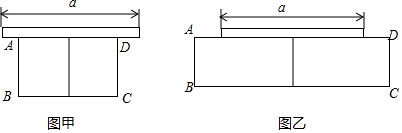
①按图甲的方案,要围成面积为25平方米的花圃,则AD的长是多少米?
②按图乙的方案,能围成的矩形花圃的最大面积是多少?