 B .
B .  D .
D . 
① x是正方形的边长,y是这个正方形的面积;② x是矩形的一边长,y是这个矩形的周长;③ x是一个正数,y是这个正数的平方根;④ x是一个正数,y是这个正数的算术平方根.

| 甲 | 0 | 1 | 2 | 0 | 2 |
| 乙 | 2 | 1 | 0 | 1 | 1 |
关于以上数据的平均数、中位数、众数和方差,说法错误的是( )
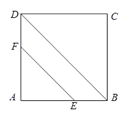
甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是( )
 B .
B . 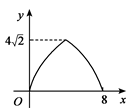 C .
C . 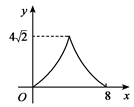 D .
D . 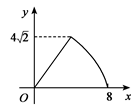
|
弹簧总长L(cm) |
16 |
17 |
18 |
19 |
20 |
|
重物质量x(kg) |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
当重物质量为4kg(在弹性限度内)时,弹簧的总长L(cm)是.





已知:平行四边形ABCD .
求作:点M , 使点M 为边AB 的中点.
作法:如图,
①作射线DA;
②以点A 为圆心,BC长为半径画弧,
交DA的延长线于点E;
③连接EC 交AB于点M .
所以点M 就是所求作的点.

根据小明设计的尺规作图过程,
证明:连接AC , EB .
∵四边形ABCD 是平行四边形,
∴AE∥BC .
∵AE= ,
∴四边形EBCA 是平行四边形( )(填推理的依据) .
∴AM =MB ( )(填推理的依据) .
∴点M 为所求作的边AB的中点.
① 当b=4时,直接写出△OBC内的整点个数;
②若△OBC内的整点个数恰有4个,结合图象,求b的取值范围.

探究函数y随自变量x的变化而变化的规律.
|
x/cm |
0 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
4.5 |
|
y/cm |
0 |
0.4 |
0.8 |
1.2 |
1.6 |
1.7 |
1.6 |
1.2 |
0 |
(要求:补全表格,相关数值保留一位小数)


已知C(-2,2),D(1,2),E(1,0),F(-2,0).
