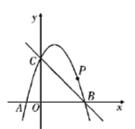
B .
B .  C .
C .  D .
D . 


![]()


抽取了某校部分教师进行了笔试理论测试,并根据测试成绩绘制成下面两幅不完整的统计图:
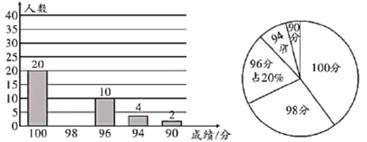
请根据统计图中提供的信息,回答下面的问题:

|
果园 |
路程/千米 |
|
|
甲仓库 |
乙仓库 |
|
|
A |
15 |
25 |
|
B |
20 |
20 |
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元。