安徽省六安市寿县2018-2019学年八年级下学期数学期末考...

更新时间：2020-06-03 浏览次数：190 类型：期末考试

一、选择题

1. (2019八下·寿县期末) 当 $\text{[math]}$ 有意义时，a的取值范围是（　　）

A . a≥2 B . a＞2 C . a≠2 D . a≠-2

答案解析收藏纠错 + 选题
2. (2020八上·富平期末) 在某市举办的垂钓比赛上，5名垂钓爱好者参加了比赛，比赛结束后，统计了他们各自的钓鱼条数，成绩如下：4，5，10，6，10．则这组数据的中位数是（　　）

A . 5 B . 6 C . 7 D . 10

答案解析收藏纠错 + 选题
3. (2019八下·寿县期末) 下列各式计算正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2019八下·寿县期末) 已知2是关于x的方程x²-2ax+4=0的一个解，则a的值是（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
5. (2019八下·寿县期末) 数据-2，-1，0，1，2的方差是（　　）

A . $\text{[math]}$ B . 2 C . 1 D . 2.5

答案解析收藏纠错 + 选题
6. (2019八下·寿县期末) 将一张平行四边形的纸片折一次，使得折痕平分这个平行四边形的面积．则这样的折纸方法共有（　　）

A . 1种 B . 2种 C . 4种 D . 无数种

答案解析收藏纠错 + 选题
7. (2019八下·寿县期末) 下列说法中不正确的是（　　）

A . 一组对边平行且一组对角相等的四边形是平行四边形 B . 每组邻边都相等的四边形是菱形 C . 四个角都相等的四边形是矩形 D . 对角线互相垂直平分的四边形是正方形

答案解析收藏纠错 + 选题
8. (2019八下·寿县期末) 已知一元二次方程x²-2x-1=0的两根分别为x₁ ， x₂ ，则 $\text{[math]}$ + $\text{[math]}$ 的值为（　　）

A . 2 B . -1 C . $\text{[math]}$ D . -2

答案解析收藏纠错 + 选题
9. (2023八下·临沂期中) 如图，将两个大小、形状完全相同的△ABC和△A′B′C′拼在一起，其中点A′与点A重合，点C′落在边AB上，连接B′C．若∠ACB=∠AC′B′=90°，AC=BC=3，则B′C的长为（）

A . 3 $\text{[math]}$ B . 6 C . 3 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019八下·寿县期末) 在△ABC中，AB=BC=2，O是线段AB的中点，P是射线CO上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为（　　）

A . 1， $\text{[math]}$ ，7 B . 1， $\text{[math]}$ ， $\text{[math]}$ C . 1， $\text{[math]}$ D . 1，3， $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020八上·香洲期末) 正六边形的每个内角等于°．

答案解析收藏纠错 + 选题
12. (2019八下·寿县期末) 若关于x的一元二次方程(k-1)x²+4x+1=0有实数根，则k的取值范围是

答案解析收藏纠错 + 选题
13. (2019八下·寿县期末) 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=8，AB=5，则AE的长为．

答案解析收藏纠错 + 选题
14. 如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是边BM、CM的中点，当AB：AD=时，四边形MENF是正方形．

答案解析收藏纠错 + 选题

三、计算题

15. (2019八下·寿县期末) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2019八下·寿县期末) 解方程：x（x-3）=4．

答案解析收藏纠错 + 选题

四、解答题（本大题共 7 小题，共 74 分）

17. (2019八下·寿县期末)
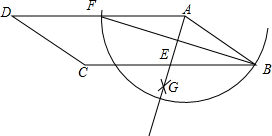
如图，在方格纸中，点A，B，P都在格点上．请按要求画出以AB为边的格点四边形，使P在四边形内部（不包括边界上），且P到四边形的两个顶点的距离相等．
1. （1）在图甲中画出一个▱ABCD．
2. （2）在图乙中画出一个四边形ABCD，使∠D=90°，且∠A≠90°．（注：图甲、乙在答题纸上）
答案解析收藏纠错 + 选题
18. (2020九上·西工期中) 如图，一次函数y=kx+b的图象经过（2，4）、（0，2）两点，与x轴相交于点C．求：
1. （1）此一次函数的解析式；
2. （2） △AOC的面积．
答案解析收藏纠错 + 选题
19. (2019八下·寿县期末) 若关于x的一元二次方程x²-2（2-k）x+k²+12=0有实数根α、β．
1. （1）求实数k的取值范围；
2. （2）设 $\text{[math]}$ ，求t的最小值．
答案解析收藏纠错 + 选题

20. (2019八下·寿县期末) 某校举行了“文明在我身边”摄影比赛，已知每幅参赛作品成绩记为x分（60≤x≤100）．校方从600幅参赛作品中随机抽取了部分步赛作品，统计了它们的成绩，并绘制了如下不完整的统计图表．

“文明在我身边”摄影比赛成绩统计表

分数段	频数	频率
60≤x＜70	18	0.36
70≤x＜80	17	c
80≤x＜90	a	0.24
90≤x≤100	b	0.06
合计		1

根据以上信息解答下列问题：

（1）统计表中a=，b=，c=．
（2）补全数分布直方图；
（3）若80分以上的作品将被组织展评，试估计全校被展评作品数量是多少？

答案解析收藏纠错 + 选题

21. (2019八下·寿县期末) 矩形ABCD中，E、F分别是AD、BC的中点，CE、AF分别交BD于G、H两点．

求证：
1. （1）四边形AFCE是平行四边形；
2. （2） EG=FH．
答案解析收藏纠错 + 选题
22. (2019八下·寿县期末) 随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位不断增加．
1. （1）该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个，求该市这两年（从2013年度到2015年底）拥有的养老床位数的平均年增长率；
2. （2）若该市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间（1个养老床位），双人间（2个养老床位），三人间（3个养老床位），因实际需要，单人间房间数在10至30之间（包括10和30），且双人间的房间数是单人间的2倍，设规划建造单人间的房间数为t．
  ①若该养老中心建成后可提供养老床位200个，求t的值；
  ②求该养老中心建成后最多提供养老床位多少个？最少提供养老床位多少个？
答案解析收藏纠错 + 选题
23. (2020八上·象山期末) 问题背景
如图1，在正方形ABCD的内部，作∠DAE=∠ABF=∠BCG=∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得到四边形EFGH是正方形．
类比探究
如图2，在正△ABC的内部，作∠BAD=∠CBE=∠ACF，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）
1. （1） △ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明．
2. （2） △DEF是否为正三角形？请说明理由．
3. （3）进一步探究发现，△ABD的三边存在一定的等量关系，设BD=a，AD=b，AB=c，请探索a，b，c满足的等量关系．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

安徽省六安市寿县2018-2019学年八年级下学期数学期末考...

副标题：

*注意事项：

安徽省六安市寿县2018-2019学年八年级下学期数学期末考...

试题分析

总体分析

题量分析

难度分析

知识点分析