
 B .
B . 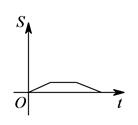 C .
C . 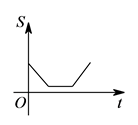 D .
D . 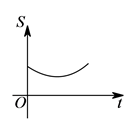


|
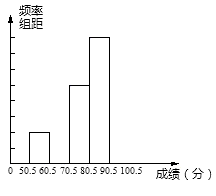
频率分布表 |
||
|
分组 |
频数 |
频率 |
|
50.5~60.5 |
4 |
0.08 |
|
60.5~70.5 |
8 |
0.16 |
|
70.5~80.5 |
10 |
0.20 |
|
80.5~90.5 |
16 |
0.32 |
|
90.5~100.5 |
||
|
合计 |
||
除图甲外,请你再给出三个不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图乙和图甲是相同的操作).

图① 图② 图③
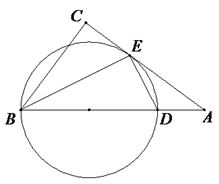
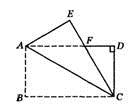
把两块边长为4的等边三角形板 和
叠放在一起,使三角形板
的顶点
与三角形板
的AC边中点
重合,把三角形板
固定不动,让三角形板
绕点
旋转,设射线
与射线
相交于点M,射线
与线段
相交于点N.
