江苏省无锡市锡北片2020年数学中考一模试卷

更新时间：2020-08-07 浏览次数：159 类型：中考模拟

一、选择题

1. -2的相反数是（）

A . 2 B . -2 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·泸县期末) 要使代数式 $\text{[math]}$ 有意义，则x的取值范围是（）

A . x≠2 B . x≥2 C . x>2 D . x≤2

答案解析收藏纠错 + 选题
3. (2020·无锡模拟) 我国倡导的“一带一路”将促进中国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总人口为 $\text{[math]}$ 人，这个数用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020九下·无锡期中) 小王在清点本班为偏远贫困地区的捐款时发现，全班同学捐款的钞票情况如下：100元的3 张，50元的9张，10元的23张，5元的10张．在这些不同面额的钞票中，众数是（）

A . 10 B . 23 C . 50 D . 100

答案解析收藏纠错 + 选题
5. (2020·无锡模拟) 如图，AB为⊙O的直径，点C在⊙O上．若∠C=16°，则∠BOC的度数是（）

A . 74° B . 48° C . 32° D . 16°

答案解析收藏纠错 + 选题
6. (2020·无锡模拟) 下列命题中错误的是（）

A . 两组对边分别相等的四边形是平行四边形 B . 对角线相等的平行四边形是矩形 C . 一组邻边相等的平行四边形是菱形 D . 对角线垂直相等的四边形是正方形

答案解析收藏纠错 + 选题
7. (2020·无锡模拟) 若圆锥的主视图是边长为 $\text{[math]}$ 的等边三角形，则该圆锥俯视图的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·无锡模拟)
如图，正六边形ABCDEF内接于⊙O，若直线PA与⊙O相切于点A，则∠PAB=（　　）

A . 30° B . 35° C . 45° D . 60°

答案解析收藏纠错 + 选题
9. (2020·无锡模拟) 一次函数y＝x－b的图像，沿着过点（1，0）且垂直于x轴的直线翻折后经过点（4，1），则b的值为（）

A . －5 B . 5 C . －3 D . 3

答案解析收藏纠错 + 选题
10. (2020·无锡模拟) 已知正方形ABCD的边长为5，E在BC边上运动，DE的中点G，EG绕E顺时针旋转90°得EF，问CE为多少时A，C，F在一条直线上（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020·无锡模拟) 分解因式：x²﹣4=．

答案解析收藏纠错 + 选题
12. (2024九下·茂南期中) 方程 $\text{[math]}$ = 1的解是．

答案解析收藏纠错 + 选题
13. (2024八上·白城月考) 一个正八边形的每个外角等于度.

答案解析收藏纠错 + 选题
14. (2020·无锡模拟) 已知方程x²﹣3x+k=0有两个相等的实数根，则k=.

答案解析收藏纠错 + 选题
15. (2020·无锡模拟) 某楼盘2015年房价均价为每平方米8000元，经过两年连续涨价后，2017年房价均价为15000元.设该楼盘这两年房价平均增长率为x，根据题意可列方程为．

答案解析收藏纠错 + 选题
16. (2020·无锡模拟) 若函数y=kx﹣b的图象如图所示，则关于x的不等式k（x﹣3）﹣b＞0的解集是.

答案解析收藏纠错 + 选题
17. (2020·无锡模拟) 在平面直角坐标系中，已知A（3，0），B是以M（3，4）为圆心，1为半径的圆周上的一个动点，连结BO，设BO的中点为C，则线段AC的最小值为．

答案解析收藏纠错 + 选题
18. (2020九上·宝安期中) 如图，已知点A是第一象限内横坐标为 $\text{[math]}$ 的一个定点，AC⊥x轴于点M，交直线y=－x于点N.若点P是线段ON上的一个动点，∠APB=30°，BA⊥PA，则点P在线段ON上运动时，A点不变，B点随之运动.求当点P从点O运动到点N时，点B运动的路径长是.

答案解析收藏纠错 + 选题

三、解答题

19. (2020·无锡模拟) 计算：
1. （1） 2^-2+ $\text{[math]}$ ﹣ $\text{[math]}$ sin30°；
2. （2）（1+ $\text{[math]}$ ）÷ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2020·无锡模拟)
1. （1）解方程：x²﹣6x+4=0；
2. （2）解不等式组 $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2020·无锡模拟)
如图，在▱ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．
1. （1）求证：△AEB≌△CFD
2. （2）若四边形EBFD是菱形，求∠ABD的度数
答案解析收藏纠错 + 选题
22. (2020·无锡模拟) 如图
1. （1）如图，将A、B、C三个字母随机填写在三个空格中（每空填一个字母，每空中的字母不重复），请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率；
2. （2）若在如图三个空格的右侧增加一个空格，将A、B、C、D四个字母任意填写其中（每空填一个字母，每空中的字母不重复），从左往右字母顺序恰好是A、B、C、D的概率为.
答案解析收藏纠错 + 选题
23. (2020·无锡模拟) 某区教育局为了解今年九年级学生体育测试情况，随机抽查了某班学生的体育测试成绩为样本，按A、B、C、D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：
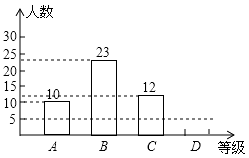
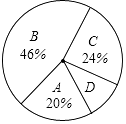
说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下
1. （1）样本中D级的学生人数占全班学生人数的百分比是；
2. （2）扇形统计图中A级所在的扇形的圆心角度数是；
3. （3）请把条形统计图补充完整；
4. （4）若该校九年级有500名学生，请你用此样本估计体育测试中A级和B级的学生人数之和．
答案解析收藏纠错 + 选题
24. (2020·石嘴山模拟) 已知：如图，在△ABC中，AB＝AC，AE是角平分线，BM平分∠ABC交AE于点M，经过B，M两点的⊙O交BC于点G，交AB于点F，FB恰为⊙O的直径.
1. （1）求证：AE与⊙O相切；
2. （2）当BC＝4，cosC＝ $\text{[math]}$ 时，求⊙O的半径.
答案解析收藏纠错 + 选题
25. (2020·无锡模拟) 某校八年级学生小丽、小强和小红到某超市参加了社会实践活动，在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克，下面是他们在活动结束后的对话.
小丽：如果以10元/千克的价格销售，那么每天可售出300千克.

小强：如果每千克的利润为3元，那么每天可售出250千克.

小红：如果以13元/千克的价格销售，那么每天可获取利润750元.

（利润=（销售价-进价）销售量）
1. （1）请根据他们的对话填写下表：
  
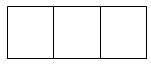
  销售单价x（元/kg）
  
  10
  
  11
  
  13
  
  销售量y（kg）
2. （2）请你根据表格中的信息判断每天的销售量y（千克）与销售单价x（元）之间存在怎样的函数关系.并求y（千克）与x（元）（x＞0）的函数关系式；
3. （3）设该超市销售这种水果每天获取的利润为W元，求W与x的函数关系式.当销售单价为何值时，每天可获得的利润最大？最大利润是多少元？
答案解析收藏纠错 + 选题
26. (2020·无锡模拟) 如图，已知△ABC（AC＜AB＜BC），请用直尺（不带刻度）和圆规，按下列要求作图（不要求写作法，但要保留作图痕迹）：
1. （1）在边BC上确定一点P，使得PA+PC=BC；
2. （2）作出一个△DEF，使得：①△DEF是直角三角形；②△DEF的周长等于边BC的长。
答案解析收藏纠错 + 选题
27. (2020·无锡模拟) 如图，在平面直角坐标系xOy中，抛物线y=ax²﹣2x+c与直线y=﹣ $\text{[math]}$ x+3分别交于x轴、y轴上的B、C两点，抛物线的顶点为点D，联结CD交x轴于点E.
1. （1）求抛物线的解析式以及点D的坐标；
2. （2）求tan∠BCD；
3. （3）点P在直线BC上，若∠PEB=∠BCD，求点P的坐标.
答案解析收藏纠错 + 选题
28. (2020·无锡模拟) 如图，在平面直角坐标系中，点A的坐标为（6，0），点B的坐标为（0，2），点M从点A出发沿x轴负方向以每秒3cm的速度移动，同时点N从原点出发沿y轴正方向以每秒1cm的速度移动.设移动的时间为t秒.
1. （1）若点M在线段OA上，试问当t为何值时，△ABO与以点O、M、N为顶点的三角形相似？
2. （2）若直线y=x与△OMN外接圆的另一个交点是点C.
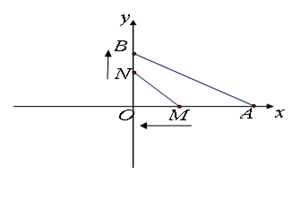
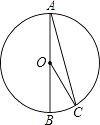
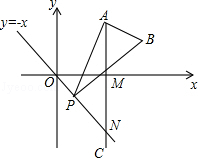
  ①试说明：当0<t<2时，OM、ON、OC在移动过程满足OM+ON= $\text{[math]}$ OC；
  
  ②试探究：当t>2时，OM、ON、OC之间的数量关系是否发生变化，并说明理由.
答案解析收藏纠错 + 选题