一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的
-
A .  B .
B .  C . 2020
D . -2020
C . 2020
D . -2020
-
2.
(2020·上城模拟)
国家发展改革委3月2日宣布,包括普通口罩、医用口罩、医用N95口罩在内,全国口罩日产量达到116 000 000只。116 000 000用科学记数法可以表示为( )
A . 1.16×108
B . 1.16×109
C . 11.6×107
D . 0.116×109
-
3.
(2020·上城模拟)
如图,在

ABCD中,AB=6,BC=4,BE平分∠ABC,交CD于点E,则DE的长度是( )
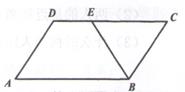
A .  B . 2
C .
B . 2
C .  D . 3
D . 3
-
A . 2x²+x=3x3
B . 2x²-7x²=-5
C . -8x3·4x2=-32x6
D .  =x²
=x²
-
5.
(2020·上城模拟)
某校开展了“空中云班会”的满意度调查,其中九年级各班满意的人数分别为27,28,28,29,29,30。下列关于这组数据描述正确的是( )
A . 中位数是29
B . 众数是28
C . 平均数为28.5
D . 方差是2
-
6.
(2020·上城模拟)
如图,在△ABC中,AB=AC,BE⊥AC,D是AB中点,且DE=BE。则∠C的度数是( )
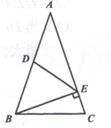
A . 65°
B . 70°
C . 75°
D . 80°
-
7.
(2021八上·营口期末)
“杭州城市大脑”用大数据改善城市交通,实现了从治堵到治城的转变.数据表明,杭州上塘高架路上共22km的路程,利用城市大脑后,车辆通过速度平均提升了15%,节省时间5分钟。设提速前车辆平均速度为xkm/h,则下列方程正确的是( )
-
8.
(2021·越城模拟)
一把5m长的梯子AB斜靠在墙上,梯子倾斜角α的正切值为

,考虑安全问题,现要求将梯子的倾斜角改为30°,则梯子下滑的距离AA'的长度是( )
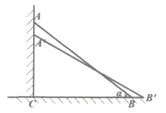
-
-
10.
(2020·上城模拟)
如图,在菱形ABCD中,∠ABC=60°,点P在对角线BD上(不与点B,D重合),PE∥BC,PF∥DC。设AB=m,AP=a,PF=b,PE=c,下列表述正确的是( )

A . c²+b²=a2
B . a+b=c+m
C . c²+b²-bc=a²
D . a+b+c≥2m
二、填空题:本大题有6个小题,每小题4分,共24分.
-
-
-
13.
(2020·上城模拟)
在国新办4月2日举行的疫情期间中国海外留学人员安全问题新闻发布会上,外交部副部长马朝旭透露,3月份全球疫情加速扩散后,中国已经安排A与B两种型号的包机9架次,从伊朗、意大利等国接回包括留学人员在内的中国公民1457人。其中A型包机每架次坐满158人,B型包机每架次坐满163人,则A型包机有
架,B型包机有
架。
-
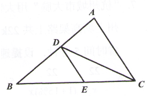
14.
(2020·包头模拟)
如图,△ABC中,D,E两点分别在边AB,BC上,若AD:DB=CE:EB=3:4,记△DBE的面积为S
1 , △ADC的面积为S
2 , 则S
1:S
2=
。
-
15.
(2020·上城模拟)
当-1≤a≤

时,则抛物线y=-x²+2ax+2-a的顶点到x轴距离的最小值
。
-
16.
(2020·上城模拟)
已知点C在线段AB的中垂线上,连结BC,点D为BC的中点,以点A为圆心,AD长为半径作⊙A。设k=

,若⊙A与线段BC有两个交点(包括点B和点C),则k满足的条件是
。
三、解答题:本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤。
-
-
(1)
计算:-4+3-

;
-
(2)
化简:

,并从0,1,2中选一个合适的数作为x的值代入求值。
-
18.
(2020·上城模拟)
2020年春,因为新冠肺炎的影响,浙江省推行“停课不停学”的举措,师生进行网络教学。九年级的小陈同学在家收到了学校邮寄过来的语文、数学、英语、科学等四个学科的课本。求下列事件发生的概率。
-
(1)
事件A:小陈同学从快递包里随机取出一本,取出的课本是数学课本;
-
(2)
事件B:小陈同学从快递包里随机取出两本,取出的课本是语文课本和数学课本。
-
19.
(2020·上城模拟)
如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点D,过D作DE⊥AB于点F,交CB的延长线于点E。
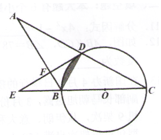
-
-
(2)
若EF=

,EB=2,求图中阴影的面积。
-
20.
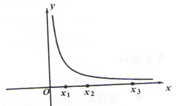
(2020·上城模拟)
已知x
1 , x
2 , x
3是y=

图像上三个点的横坐标,且满足x
3>x
2>x
1>0。请比较

与

的大小,并说明理由。
-
21.
(2020·上城模拟)
黄金分割为“最美丽”的几何比率,广泛应用于图案设计。下图是一个包装盒的俯视图,线段AB是这个俯视图的中轴线,某公司想在中轴线AB上找到黄金分割点,安装视频播放器。

-
(1)
请你用尺规作图的方式找出这个点(作出一点即可,保留作图痕迹);
-
-
22.
(2020·上城模拟)
同学A在离学校正北30km处,骑车以15km/h的速度向学校方向出发,同时,B同学在学校的正东15km处,以15km/h的速度骑车向学校方向前进,假设2人的行驶方向和速度都不变,问:
-
(1)
当其中一人经过学校时,另一人与学校之间的距离为多少?
-
-
-
23.
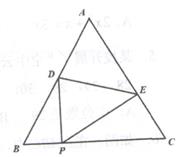
(2020·上城模拟)
如图,在等边三角形ABC中,BC=8,过BC边上一点P,作∠DPE=60°,分别与边AB,AC相交于点D与点E。
-
(1)
在图中找出与∠EPC始终相等的角,并说明理由;
-
(2)
若△PDE为正三角形时,求BD+CE的值;
-
(3)
当DE∥BC时,请用BP表示BD,并求出BD的最大值。

 B .
B .  C .
C .  D .
D . 





