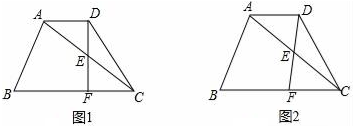
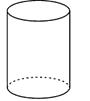
 B .
B .  C .
C .  D .
D . 

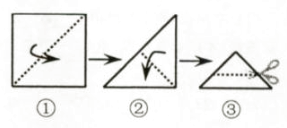
 B .
B . 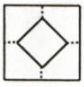 C .
C .  D .
D . 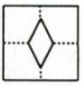
第二次:作点A1关于x轴的对称点A2;
第三次:将点A2绕点O逆时针旋转90°得到A3;
第四次:作点A3关于x轴的对称点A4…,
按照这样的规律,点A35的坐标是( )





解:去分母得:3(1+x)﹣2(2x+1)≤1①去括号得:3+3x﹣4x+1≤1②
移项得:3x﹣4x≤1﹣3﹣1③合并同类项得:﹣x≤﹣3④
两边都除以﹣1得:x≤3⑤

收集数据
从八、九两个年级各随机抽取20名学生,进行了体质健康测试,测试成绩(百分制)如下:
|
八年级 |
78 |
86 |
74 |
81 |
75 |
76 |
87 |
70 |
75 |
90 |
|
75 |
79 |
81 |
70 |
74 |
80 |
86 |
69 |
83 |
77 |
|
|
九年级 |
93 |
73 |
88 |
81 |
72 |
81 |
94 |
83 |
77 |
83 |
|
80 |
81 |
70 |
81 |
73 |
78 |
82 |
80 |
70 |
40 |
整理、描述数据
按如下分数段整理、描述 这两组样本数据:
|
成绩 人数x 部门 |
40≤x≤49 |
50≤x≤59 |
60≤x≤69 |
70≤x≤79 |
80≤x≤89 |
90≤x≤100 |
|
八年级 |
0 |
0 |
1 |
11 |
|
1 |
|
九年级 |
1 |
0 |
0 |
7 |
|
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
|
年级 |
平均数 |
中位数 |
众数 |
方差 |
|
八年级 |
78.3 |
77.5 |
75 |
33.6 |
|
九年级 |
78 |
80.5 |
|
52.1 |