 B .
B .  C .
C .  D .
D . 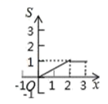 B .
B . 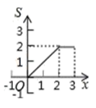 C .
C . 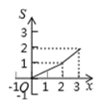 D .
D . 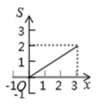
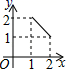 B .
B . 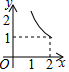 C .
C . 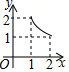 D .
D . 
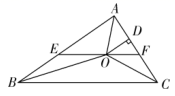
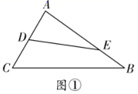
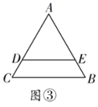
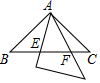
①若 ,
;
② ;
③ 平分
;
④若 ,
,则
.
其中正确的有.(把所有正确结论的序号都选上)
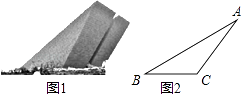
位于合肥滨湖新区的渡江战役纪念馆,实物图如图1所示,示意图如图2所示.某学校数学兴趣小组通过测量得知,纪念馆外轮廓斜坡AB的坡度i=1: ,底基BC=50m,∠ACB=135°,求馆顶A离地面BC的距离.(结果精确到0.1m,参考数据:
≈1.41,
≈1.73)