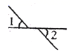
 C .
C . 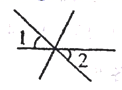 D .
D . 


① ;②
平分
;③
;④
.
请将正确结论的序号填写在空中,并选择其一证明.
正确结论的序号是,我选择证明的结论序号是,证明:

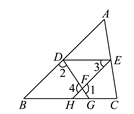
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,过点E作EH⊥EF,垂足为E,交CD于H点. 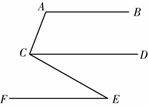
小明想了许久对于求∠CEH的度数没有思路,就去请教好朋友小丽,小丽给了他如图2所示的提示:
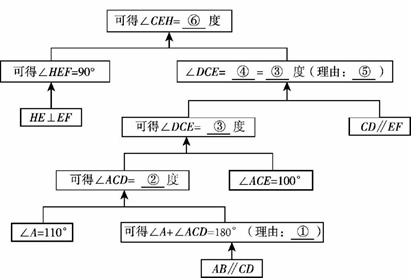
请问小丽的提示中理由①是;
提示中②是:度;
提示中③是:度;
提示中④是:,理由⑤是.
提示中⑥是度;

一动点沿着数轴向右平移 个单位,再向左平移
个单位,相当于向右平移
个单位.用有理数加法表示为
.若坐标平面上的点做如下平移:沿
轴方向平移的数量为
(向右为正,向左为负,平移
个单位),沿
轴方向平移的数量为
(向上为正,向下为负,平移
个单位),则把有序数对
叫做这一平移的“平移量”;“平移量”
与“平移量”
的加法运算法则为
解决问题:
⑴计算: ;
⑵动点 从坐标原点
出发,先按照“平移量”
平移到
,再按照“平移量”
平移到
:若先把动点
按照.“平移量”
平移到
,再按照“平移量”
平移,最后的位置还是
吗?在图1中画出四边形
.
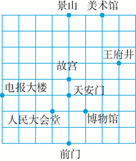
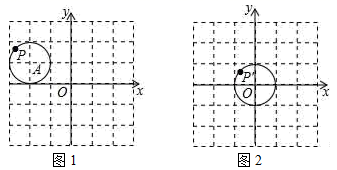
⑶如图2,一艘船从码头 出发,先航行到湖心岛码头
,再从码头
航行到码头
,最后回到出发点
.请用“平移量”加法算式表示它的航行过程.


解:⑴ ;
⑵答:;
⑶加法算式:.

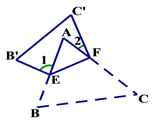
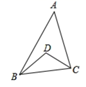
探究:在图2中, 、
分别为四边形
的边
、
的中点,四边形
的面积记为
,阴影部分面积记为
,则
和
之间满足的关系式为:
在图3中, 、
、
、
分别为任意四边形
的边
、
、
、
的中点,并且图中阴影部分的面积为
平方厘米,求图中四个小三角形的面积和,并说明理由.