初中数学浙教版八年级上册第4章图形与坐标单元检测（提高篇...

更新时间：2020-08-17 浏览次数：265 类型：单元试卷

一、单选题

1. 下列关于有序数对的说法正确的是（）

A . （3，4）与（4，3）表示的位置相同 B . （a，b）与（b，a）表示的位置肯定不同 C . （3，5）与（5，3）是表示不同位置的两个有序数对 D . 有序数对（2，2）与（2，2）表示两个不同的位置

答案解析收藏纠错 + 选题
2. (2019七下·阜阳期中) 如图，军训时七(1)班的同学按教官的指令站了7排8列，如果第7排第8列的同学的位置在队列的东北角，可以用有序数对(7，8)来表示，那么表示站在西南角同学的位置的有序数对是（）

A . (7，8) B . (1，1) C . (1，2) D . (2，1)

答案解析收藏纠错 + 选题
3. (2019·莆田模拟) 点A（x ， y）为平面直角坐标系内一点，其中x ， y满足3，x+2，y﹣4中的两个数相等，则所有的点A组成的图形为（）

A . 一个点 B . 两条相交的直线 C . 一个三角 D . 相交于一点的三条直线

答案解析收藏纠错 + 选题
4. (2023八上·达川期末) 下列说法中，正确的是（）．
①在平面内，两条互相垂直的数轴，组成了平面直角坐标系；②如果点 $\text{[math]}$ 到 $\text{[math]}$ 轴和 $\text{[math]}$ 轴的距离分别为 $\text{[math]}$ ， $\text{[math]}$ ，且点 $\text{[math]}$ 在第一象限，那么 $\text{[math]}$ ；③如果点 $\text{[math]}$ 位于第四象限，那么 $\text{[math]}$ ；④如果点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，那么点 $\text{[math]}$ 到坐标原点的距离为 $\text{[math]}$ ；⑤如果点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，那么点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ．

A . ②③④ B . ②④⑤ C . ①③⑤ D . ②③⑤

答案解析收藏纠错 + 选题
5. (2021八下·武进月考) 在平面直角坐标系中，点A（a，0），点B（2﹣a，0），且A在B的左边，点C（1，﹣1），连接AC，BC，若在AB，BC，AC所围成区域内（含边界），横坐标和纵坐标都为整数的点的个数为4个，那么a的取值范围为（）

A . ﹣1＜a≤0 B . 0≤a＜1 C . ﹣1＜a＜1 D . ﹣2＜a＜2

答案解析收藏纠错 + 选题
6. (2023八上·凤翔期末) 已知点 $\text{[math]}$ 关于x轴的对称点和点 $\text{[math]}$ 关于y轴的对称点相同，则点 $\text{[math]}$ 关于x轴对称的点的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7.
如图，在平面直角坐标系中，△ABC与△DEF关于直线m=1对称，点M、N分别是这两个三角形中的对应点，如果点M的横坐标是a，那么点N的横坐标是（　　）

A . ﹣a B . ﹣a+1 C . a+2 D . ﹣a+2

答案解析收藏纠错 + 选题
8. (2020·上虞模拟) 如图，在平面直角坐标系xO₁y中，点A的坐标为(1，1)。如果将x轴向上平移3个单位长度，将y轴向左平移2个单位长度，交于点Q，点A的位置不变，那么在平面直角坐标系xO₂y中，点A的坐标是（）

A . (-3，2) B . (3，-2) C . (-2，-3) D . (3，4)

答案解析收藏纠错 + 选题
9. (2019·菏泽) 在平面直角坐标系中，一个智能机器人接到的指令是：从原点 $\text{[math]}$ 出发，按“向上→向右→向下→向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点 $\text{[math]}$ ，第二次移动到点 $\text{[math]}$ ……第 $\text{[math]}$ 次移动到点 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2018八上·佳木斯期中) 如图，在平面直角坐标系上有个点A（-1，0），点A第1次向上跳动一个单位至点A₁（-1，1），紧接着第2次向右跳动2个单位至点A₂（1，1），第3次向上跳动1个单位，第4次向左跳动3个单位，第5次又向上跳动1个单位，第6次向右跳动4个单位，…，依次规律跳动下去，点A第2017次跳动至点A₂₀₁₇的坐标是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

11. (2018七上·无锡期中) 将正整数从1开始，按如图所表示的规律排列．规定图中第m行、第n列的位置记作(m，n)，如正整数8的位置是(2，3)，则正整数139的位置记作．

答案解析收藏纠错 + 选题
12. (2021八下·卢龙期末) 学校位于小亮家北偏东35方向，距离为300m，学校位于大刚家南偏东85°方向，距离也为300m，则大刚家相对于小亮家的位置是.

答案解析收藏纠错 + 选题
13. (2020·北京模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，我们把横、纵坐标都是整数的点为“整点”，已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 在轴的上方， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 内部（不含边界）的整点的个数为．

答案解析收藏纠错 + 选题
14. (2019七下·铜陵期末) 如图所示，直线BC经过原点O，点A在x轴上，AD⊥BC于D，若B（m，3），C（n，-5），A（4，0），则AD•BC=．

答案解析收藏纠错 + 选题
15. (2020·达县) 如图，点 $\text{[math]}$ 与点 $\text{[math]}$ 关于直线 $\text{[math]}$ 对称，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2018八上·北京月考) 平面直角坐标系中有一点A（1，1）对点A进行如下操作：
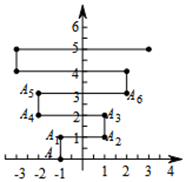
第一步，作点A关于x轴的对称点A₁ ，延长线段AA₁到点A₂ ，使得2A₁A₂=AA₁；

第二步，作点A₂关于y轴的对称点A₃ ，延长线段A₂A₃到点A₄ ，使得2A₃A₄=A₂A₃；

第三步，作点A₄关于x轴的对称点A₅ ，延长线段A₄A₅到点A₆ ，使得2A₅A₆=A₄A₅；

……

则点A₂的坐标为，点A₂₀₁₅的坐标为；

若点A_n的坐标恰好为（4^m ， 4ⁿ）（m、n均为正整数），请写出m和n的关系式．

答案解析收藏纠错 + 选题

三、解答题

17. (2024九下·宜春模拟) 若点 $\text{[math]}$ 的坐标为（ $\text{[math]}$ ， $\text{[math]}$ ），其中 $\text{[math]}$ 满足不等式组 $\text{[math]}$ ，
求点 $\text{[math]}$ 所在的象限.

答案解析收藏纠错 + 选题
18. 温州一位老人制作的仿真郑和宝船尺寸如图，已知在某一直角坐标系中点A坐标为（9，0），请你直接在图中画出该坐标系，并写出其余5点的坐标．

答案解析收藏纠错 + 选题
19. 如图是小丽以学校为观测点，画出的一张平面图．
1. （1）生源大酒店在学校偏方向米处．汽车站在学校偏方向米处；
2. （2）中医院在邮电局东偏北60°方向400米处，请在上图中标出它的位置；
3. （3）小丽以每分钟50米的速度步行，从汽车站经过学校.邮局再到中医院大约需要分钟．
答案解析收藏纠错 + 选题
20. (2020七下·武汉期中) 如图 1，在平面直角坐标系中，已知点A(a，0)，B(b，0)，C(2，7)，连接 AC，交y轴于 D，且 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求点D的坐标.
2. （2）如图 2，y轴上是否存在一点P，使得△ACP的面积与△ABC的面积相等？若存在，求点P的坐标，若不存在，说明理由.
3. （3）如图 3，若 Q(m，n)是 x轴上方一点，且 $\text{[math]}$ 的面积为20，试说明：7m＋3n是否为定值，若为定值，请求出其值，若不是，请说明理由.
答案解析收藏纠错 + 选题
21. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a.b满足 $\text{[math]}$ ＋|b－6|＝0，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O－C－B－A－O的线路移动．
1. （1） a＝，b＝，点B的坐标为；
2. （2）当点P移动4秒时，请指出点P的位置，并求出点P的坐标；
3. （3）在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间．
答案解析收藏纠错 + 选题
22. (2017七下·马山期末)
已知△A′B′C′是由△ABC经过平移得到的，它们各顶点在平面直角坐标系中的坐标如下表所示：
△ABC
A（a，0）
B（3，0）
C（5，5）
△A′B′C′
A′（4，2）
B′（7，b）
C′（c，7）
1. （1）观察表中各对应点坐标的变化，并填空：a=，b=，c=；
2. （2）在平面直角坐标系中画出△ABC及平移后的△A′B′C′；
3. （3）直接写出△A′B′C′的面积是．
答案解析收藏纠错 + 选题
23. (2019八上·黑龙江期末) 如图，直线MN与x轴、y轴分别相交于B、A两点，OA，OB的长满足式子 $\text{[math]}$
1. （1）求A，B两点的坐标；
2. （2）若点O到AB的距离为 $\text{[math]}$ ，求线段AB的长；
3. （3）在（2）的条件下。x轴上是否存在点p使 $\text{[math]}$ 以AB为等腰三角形，若存在，请直接写出满足条件的点p的坐标。
答案解析收藏纠错 + 选题
24. (2018八上·青山期中) 如图1，点A(2，1)，点A与点B关于y轴对称，AC∥y轴，且AC=3，连接BC交y轴于点D.
1. （1）点B的坐标为，点C的坐标为；
2. （2）如图2，连接OC，OC平分∠ACB，求证：OB⊥OC；
3. （3）如图3，在（2）的条件下，点P为OC上一点，且∠PAC=45°，求点P的坐标.
答案解析收藏纠错 + 选题