北京2020年中考数学实战模拟测试卷三

更新时间：2020-04-29 浏览次数：262 类型：中考模拟

一、选择题（本题共16分,每小题2分,第1-8题均有四个选。正确选项只有一个。）

1. (2022七上·张家口期末) 天文单位是天文学中计量天体之间距离的一种单位，其数值取地球与太阳之间的平均距离，即149597870700m，约为149600000km.将数149600000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·吉安期中) 下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（）

A . 赵爽弦图 B . 笛卡尔心形线 C . 科克曲线 D . 斐波那契螺旋线

答案解析收藏纠错 + 选题
3. (2022九下·汕头期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020·北京模拟) 关于的不等式 $\text{[math]}$ 只有2个正整数解，则的取值范围为 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020·北京模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，依据尺规作图的痕迹，计算 $\text{[math]}$ 的度数是（）

A . 67°29′ B . 67°9′ C . 66°29′ D . 66°9′

答案解析收藏纠错 + 选题
6. (2020·北京模拟) 化简 $\text{[math]}$ 的结果是 $\text{[math]}$ 　　 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020·北京模拟) 下列说法正确是 $\text{[math]}$ 　　 $\text{[math]}$
①函数 $\text{[math]}$ 中自变量的取值范围是 $\text{[math]}$ ．

②若等腰三角形的两边长分别为3和7，则第三边长是3或7．

③一个正六边形的内角和是其外角和的2倍．

④同旁内角互补是真命题．

⑤关于的一元二次方程 $\text{[math]}$ 有两个不相等的实数根．

A . ①②③ B . ①④⑤ C . ②④ D . ③⑤

答案解析收藏纠错 + 选题
8. (2020·北京模拟) 根据《居民家庭亲子阅读消费调查报告》中的相关数据制成扇形统计图，由图可知，下列说法不正确是 $\text{[math]}$ 　　 $\text{[math]}$

A . 扇形统计图能反映各部分在总体中所占的百分比 B . 每天阅读30分钟以上的居民家庭孩子超过 $\text{[math]}$ C . 每天阅读1小时以上的居民家庭孩子占 $\text{[math]}$ D . 每天阅读30分钟至1小时的居民家庭孩子对应扇形的圆心角是 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题共16 分，每小题2 分）

9. (2020·北京模拟) 若分式 $\text{[math]}$ 有意义，则的取值范围是．

答案解析收藏纠错 + 选题
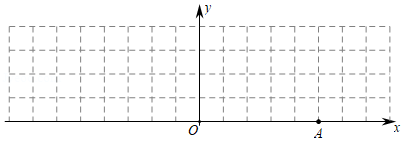
10. (2020·北京模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，我们把横、纵坐标都是整数的点为“整点”，已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 在轴的上方， $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ 内部（不含边界）的整点的个数为．

答案解析收藏纠错 + 选题
11. (2022·四川模拟) 如图是一个多面体的表面展开图，如果面 $\text{[math]}$ 在前面，从左面看是面 $\text{[math]}$ ，那么从上面看是面．（填字母）

答案解析收藏纠错 + 选题
12. (2020·北京模拟) 如图， $\text{[math]}$ △ $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
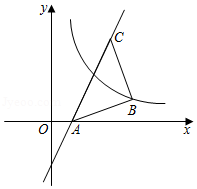
13. (2020·北京模拟) 如图，过点 $\text{[math]}$ 的直线 $\text{[math]}$ 交轴于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，曲线 $\text{[math]}$ 过点 $\text{[math]}$ ，将点 $\text{[math]}$ 沿 $\text{[math]}$ 轴正方向平移个单位长度恰好落在该曲线上，则的值为．

答案解析收藏纠错 + 选题
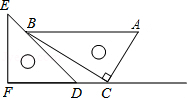
14. (2020·北京模拟) 三角板是我们学习数学的好帮手．将一对直角三角板如图放置，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长度是．

答案解析收藏纠错 + 选题
15. (2021八下·青山期末) 小刘和小李参加射击训练，各射击10次的平均成绩相同，如果他们射击成绩的方差分别是S_小刘²＝0.6，S_小李²＝1.4，那么两人中射击成绩比较稳定的是；

答案解析收藏纠错 + 选题
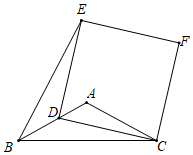
16. (2020·北京模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 上一动点 $\text{[math]}$ 点除外），以 $\text{[math]}$ 为一边作正方形 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 面积的最大值为．

答案解析收藏纠错 + 选题

三、解答题（本题共68分，第17-21题，每小题5分，第22-24题，每小题6分，第25题5分，第26题6分，第27-28题，每小题7分）

17. (2020·北京模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2022八上·灌阳期中) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2020·北京模拟) 关于的一元二次方程 $\text{[math]}$ 有实数根．
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）如果 $\text{[math]}$ 是符合条件的最大整数，且一元二次方程 $\text{[math]}$ 与方程 $\text{[math]}$ 有一个相同的根，求此时 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
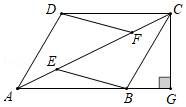
20. (2020·北京模拟) 如图，在四边形 $\text{[math]}$ 中，点 $\text{[math]}$ 和点 $\text{[math]}$ 是对角线 $\text{[math]}$ 上的两点， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积是．
答案解析收藏纠错 + 选题
21. (2020·北京模拟) 某商场统计了每个营业员在某月的销售额，绘制了如下统计图．

解答下列问题：
1. （1）设营业员的月销售额为（单位：万元）．商场规定：当 $\text{[math]}$ 时为不称职，当 $\text{[math]}$ 时为基本称职，当 $\text{[math]}$ 时为称职，当 $\text{[math]}$ 时为优秀．试求出基本称职、称职两个层次营业员人数所占百分比，并补全扇形图；
2. （2）根据（1）中规定，所有称职和优秀的营业员月销售额的中位数为，众数为；
3. （3）为了调动营业员的积极性，商场制定月销售额奖励标准，凡达到或超过这个标准的受到奖励．如果要使称职和优秀的营业员半数左右能获奖，奖励标准应定为多少万元？简述理由．
答案解析收藏纠错 + 选题
22. (2020·北京模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的高， $\text{[math]}$ 是 $\text{[math]}$ 边上的中线，且 $\text{[math]}$ ．求证：
1. （1）点 $\text{[math]}$ 在 $\text{[math]}$ 的垂直平分线上；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
23. (2020·北京模拟) 我国南宋著名数学家秦九韶在他的著作《数书九章》中提出了“三斜求积术”，三斜即指三角形的三条边长，可以用该方法求三角形面积．若改用现代数学语言表示，其形式为：设， $\text{[math]}$ ，为三角形三边， $\text{[math]}$ 为面积，则 $\text{[math]}$ ①
这是中国古代数学的瑰宝之一．

而在文明古国古希腊，也有一个数学家海伦给出了求三角形面积的另一个公式，若设 $\text{[math]}$ （周长的一半），则 $\text{[math]}$ ②
1. （1）尝试验证．这两个公式在表面上形式很不一致，请你用以5，7，8为三边构成的三角形，分别验证它们的面积值；
2. （2）问题探究．经过验证，你发现公式①和②等价吗？若等价，请给出一个一般性推导过程（可以从① $\text{[math]}$ ②或者② $\text{[math]}$ ① $\text{[math]}$ ；
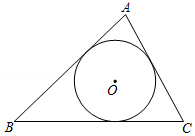
3. （3）问题引申．三角形的面积是数学中非常重要的一个几何度量值，很多数学家给出了不同形式的计算公式．请你证明如下这个公式：如图， $\text{[math]}$ 的内切圆半径为，三角形三边长为， $\text{[math]}$ ，仍记 $\text{[math]}$ ， $\text{[math]}$ 为三角形面积，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2020·北京模拟) 如图，是具有公共边 $\text{[math]}$ 的两个直角三角形，其中， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）如图1，若延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
  ①求证： $\text{[math]}$ ， $\text{[math]}$ ；
  
  ②求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 与 $\text{[math]}$ 位置如图2所示，请直接写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的数量关系．
答案解析收藏纠错 + 选题
25. (2020·北京模拟) 在平面直角坐标系中，直线 $\text{[math]}$ 交轴于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．
1. （1） $\text{[math]}$ 的值是；
2. （2）点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的一个动点，点 $\text{[math]}$ 和点 $\text{[math]}$ 分别在轴和 $\text{[math]}$ 轴上．
  ①如图，点 $\text{[math]}$ 为线段 $\text{[math]}$ 的中点，且四边形 $\text{[math]}$ 是平行四边形时，求 $\text{[math]}$ 的周长；
  
  ②当 $\text{[math]}$ 平行于轴， $\text{[math]}$ 平行于 $\text{[math]}$ 轴时，连接 $\text{[math]}$ ，若 $\text{[math]}$ 的面积为 $\text{[math]}$ ，请直接写出点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题
26. (2020·北京模拟) 某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，日销售量 $\text{[math]}$ 与时间第 $\text{[math]}$ 天之间的函数关系式为 $\text{[math]}$ ， $\text{[math]}$ 为整数），销售单价 $\text{[math]}$ （元 $\text{[math]}$ 与时间第 $\text{[math]}$ 天之间满足一次函数关系如下表：

时间第 $\text{[math]}$ 天

1

2

3

$\text{[math]}$

80

销售单价 $\text{[math]}$ （元 $\text{[math]}$

49.5

49

48.5

$\text{[math]}$

10
1. （1）直接写出销售单价 $\text{[math]}$ （元 $\text{[math]}$ 与时间第 $\text{[math]}$ 天之间的函数关系式．
2. （2）在整个销售旺季的80天里，哪一天的日销售利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
27. (2020·北京模拟) 如图1， $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 的内角 $\text{[math]}$ 、 $\text{[math]}$ 的平分线，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）如图2，如果 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）如果 $\text{[math]}$ 是锐角，且 $\text{[math]}$ 与 $\text{[math]}$ 相似，求 $\text{[math]}$ 的度数，并求出 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
28. (2020·北京模拟) 如图，抛物线 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，顶点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，与轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点．
1. （1）求抛物线的解析式．
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ 为直线 $\text{[math]}$ 上一点，当 $\text{[math]}$ 时，求点 $\text{[math]}$ 的坐标和 $\text{[math]}$ 的值．
3. （3）点 $\text{[math]}$ 是 $\text{[math]}$ 轴上一动点，当 $\text{[math]}$ 为何值时， $\text{[math]}$ 的值最小．并求出这个最小值．
4. （4）点 $\text{[math]}$ 关于轴的对称点为 $\text{[math]}$ ，当 $\text{[math]}$ 取最小值时，在抛物线的对称轴上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 是直角三角形？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题