 B .
B .  C .
C .  D .
D . 
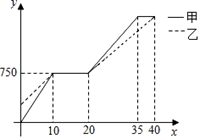
①甲、乙二人第一次相遇后,停留了10分钟;②甲先到达的目的地;③甲在停留10分钟之后提高了行走速度;④甲行走的平均速度要比乙行走的平均速度快.所有正确推断的序号是( )
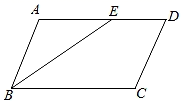
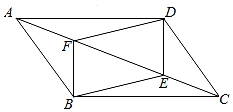
①可以得到无数个平行四边形EGFH;
②可以得到无数个矩形EGFH;
③可以得到无数个菱形EGFH;
④至少得到一个正方形EGFH .
所有正确结论的序号是.

在数学课上,老师提出如下问题:
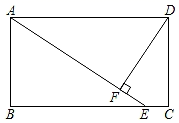
已知:如图,四边形ABCD是平行四边形.
求作:菱形AECF , 使点E , F分别在BC , AD上.

小军的作法如下:
①连接AC;
②作AC的垂直平分线EF分别交BC , AD于E , F;
③连接AE , CF .
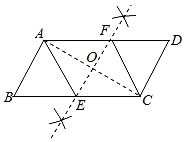
所以四边形AECF是菱形.
老师说:“小军的作法符合题意.”以下是一种证明思路,请结合作图过程补全填空,
由作图和已知可以得到:△AOF≌△COE(依据:);
∴AF=CE;
∵;
∴四边形AECF是平行四边形(依据:);
∵EF垂直平分AC;
∴(依据:);
∴四边形AECF是菱形.
由所学一次函数知识可知,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与x轴交点横坐标,是一元一次方程kx+b=0(k≠0)的解;在x轴下方的图象所对应的x的所有值是kx+b<0(k≠0)的解集,在x轴上方的图象所对应的x的所有值是kx+b>0(k≠0)的解集.例,如图1,一次函数kx+b=0(k≠0)的图象与x轴交于点A(1,0),则可以得到关于x的一元一次方程kx+b=0(k≠0)的解是x=1;kx+b<0(k≠0)的解集为x<1.结合以上信息,利用函数图象解决下列问题:
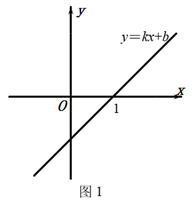
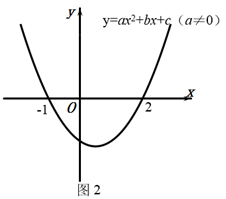
①关于x的一元二次方程ax2+bx+c=0(a≠0)的解为;
②关于x的不等式ax2+bx+c>0(a≠0)的解集为.
|
分组/分 |
频数 |
频率 |
|
50≤x<60 |
12 |
0.12 |
|
60≤x<70 |
a |
0.10 |
|
70≤x<80 |
32 |
0.32 |
|
80≤x<90 |
20 |
0.20 |
|
90≤x≤100 |
c |
b |
|
合计 |
100 |
1.00 |
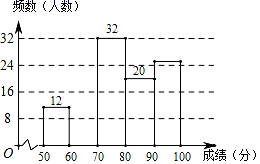
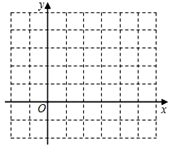
①k的值为;
②该三角形内的“整点坐标”有个;