河南省南阳市新野县2016-2017学年七年级下学期数学期末...

更新时间：2017-10-19 浏览次数：1379 类型：期末考试

一、选择题

1. (2023七下·偃师期末) 方程2x+3=7的解是（　　）

A . x=5 B . x=4 C . x=3.5 D . x=2

答案解析收藏纠错 + 选题
2. (2017七下·新野期末) 二元一次方程组 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2017七下·新野期末) 关于x，y的方程组 $\text{[math]}$ 的解是 $\text{[math]}$ ，其中y的值被盖住了，不过仍能求出p，则p的值是（）

A . ﹣ $\text{[math]}$ B . $\text{[math]}$ C . ﹣ $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2017七下·乐亭期末) 当x＜a＜0时，x²与ax的大小关系是（）

A . x²＞ax B . x²≥ax C . x²＜ax D . x²≤ax

答案解析收藏纠错 + 选题
5. (2017七下·新野期末) 如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，下列判断错误的是（）

A . AM=BM B . AP=BN C . ∠MAP=∠MBP D . ∠ANM=∠BNM

答案解析收藏纠错 + 选题
6. (2023八上·港南期末) 不等式组 $\text{[math]}$ 的解集是x＞1，则m的取值范围是（）

A . m≥1 B . m≤1 C . m≥0 D . m≤0

答案解析收藏纠错 + 选题
7. (2018·弥勒模拟) 下列图案属于轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2020九上·海东期末) 如图，将△ABC绕点A按逆时针方向旋转100°，得到△AB₁C₁ ，若点B₁在线段BC的延长线上，则∠BB₁C₁的大小为（）

A . 70° B . 80° C . 84° D . 86°

答案解析收藏纠错 + 选题
9. (2017七下·新野期末) 如图，在4×4的正方形网格中，每个小正方形的顶点称为格点，左上角阴影部分是一个以格点为顶点的正方形（简称格点正方形）．若再作一个格点正方形，并涂上阴影，使这两个格点正方形无重叠面积，且组成的图形是轴对称图形，又是中心对称图形，则这个格点正方形的作法共有（）

A . 2种 B . 3种 C . 4种 D . 5种

答案解析收藏纠错 + 选题
10. (2021八上·密山期末) 一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为（）

A . 7 B . 7或8 C . 8或9 D . 7或8或9

答案解析收藏纠错 + 选题

二、填空题

11. (2017七下·新野期末) 不等式﹣ $\text{[math]}$ x﹣1＞0的解集为．

答案解析收藏纠错 + 选题
12. (2017七下·新野期末) 如图，△ABC与△A′B′C′关于直线l对称，∠A=30°，∠C′=60°，则∠B=．

答案解析收藏纠错 + 选题
13. (2020七下·新蔡期末) 如图，D、E、F分别是△ABC三边延长线上的点，则∠D+∠E+∠F+∠1+∠2+∠3=度．

答案解析收藏纠错 + 选题
14. (2017七下·新野期末) 如图，将△ABC沿BC方向平移3cm得到△DEF，若四边形ABFD的周长为22cm，则△ABC的周长为cm．

答案解析收藏纠错 + 选题
15. (2017七下·新野期末) 已知关于x，y的二元一次方程3x﹣4y+mx+2m+8=0，若无论m取任何实数，该二元一次方程都有一个固定的解，则这个固定的解为．

答案解析收藏纠错 + 选题

三、解答题

16. (2017七下·新野期末) 解方程（不等式）组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2017七下·新野期末) 解不等式组 $\text{[math]}$ ，并写出该不等式组的最大整数解．

答案解析收藏纠错 + 选题
18. 如图所示，一个四边形纸片ABCD，∠D=90°把纸片按如图所示折叠，使点B落在AD上的B′处，AE是折痕．
1. （1）若B′E∥CD，求∠B的度数．
2. （2）在（1）的条件下，如果∠C=128°，求∠EAB的度数．
答案解析收藏纠错 + 选题
19. (2017七下·新野期末) 某校需购买一批课桌椅供学生使用，已知A型课桌椅230元/套，B型课桌椅200元/套．
1. （1）该校购买了A，B型课桌椅共250套，付款53000元，求A，B型课桌椅各买了多少套？
2. （2）因学生人数增加，该校需再购买100套A，B型课桌椅，现只有资金22000元，最多能购买A型课桌椅多少套？
答案解析收藏纠错 + 选题
20. (2017七下·新野期末) 如图，在Rt△ABC中，∠ACB=90°，点D在AB上，将△BCD绕点C按顺时针方向旋转90°后得△ECF．
1. （1）补充完成图形；
2. （2）若EF∥CD，求证：∠BDC=90°．
答案解析收藏纠错 + 选题
21. 我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决：
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：90x+ $\text{[math]}$ y=360，整理得：2x+3y=8，
我们可以找到方程的正整数解为 $\text{[math]}$ ．
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．

答案解析收藏纠错 + 选题
22. (2017七下·新野期末) 如图，已知：△ABC在正方形网格中
1. （1）请画出△ABC向左平移5个单位长度后得到的△A₁B₁C₁；
2. （2）请画出△ABC关于点O对称的△A₂B₂C₂；
3. （3）在直线MN上求作一点P，使△PAB的周长最小，请画出△PAB．
答案解析收藏纠错 + 选题
23. (2017七下·新野期末) 综合题如图①，∠DCE=∠ECB=α，∠DAE=∠EAB=β，∠D=30°，∠B=40°
1. （1） ①用α或β表示∠CNA，∠MPA，∠CNA=，∠MPA=
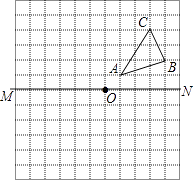
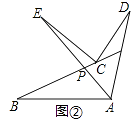
  ②求∠E的大小．
2. （2）如图②，∠BAD的平分线AE与∠BCD的平分线CE交于点E，则∠E与∠B，∠D之间是否存在某种等量关系？若存在，写出结论，说明理由；若不存在，说明理由．
答案解析收藏纠错 + 选题