河南省信阳市浉河区2020届九年级上学期数学期末考试试卷

更新时间：2024-07-13 浏览次数：167 类型：期末考试

一、单选题

1. (2020九上·浉河期末) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020九上·浉河期末) 下列方程是一元二次方程的是（）

A . $\text{[math]}$ B . x²=0 C . x²-2y=1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020九上·浉河期末) 二次函数y＝（x﹣4）²+2图象的顶点坐标是（）

A . （﹣4，2） B . （4，﹣2） C . （4，2） D . （﹣4，﹣2）

答案解析收藏纠错 + 选题
4. (2023九下·雁峰模拟) 关于x的一元二次方程x²﹣2x﹣m＝0有实根，则m的值可能是（）

A . ﹣4 B . ﹣3 C . ﹣2 D . ﹣1

答案解析收藏纠错 + 选题
5. (2020九上·浉河期末) 如图，在⊙O，点A，B，C在⊙O上，若∠OAB＝54°，则∠C（）

A . 54° B . 27° C . 36° D . 46°

答案解析收藏纠错 + 选题
6. (2021九上·东坡期末) 一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同.搅匀后任意摸出一个球，是黄球的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022九上·罗湖期中) 天虹商场一月份鞋帽专柜的营业额为100万元，三月份鞋帽专柜的营业额为150万元.设一到三月每月平均增长率为x，则下列方程正确的是（）

A . 100（1+2x）＝150 B . 100（1+x）²＝150 C . 100（1+x）+100（1+x）²＝150 D . 100+100（1+x）+100（1+x）²＝150

答案解析收藏纠错 + 选题
8. (2020九上·浉河期末) 如图，在同一平面直角坐标系中，一次函数y₁＝kx+b（k、b是常数，且k≠0）与反比例函数y₂＝ $\text{[math]}$ （c是常数，且c≠0）的图象相交于A（﹣3，﹣2），B（2，m）两点，则不等式y₁＞y₂的解集是（）

A . ﹣3＜x＜2 B . x＜﹣3或x＞2 C . ﹣3＜x＜0或x＞2 D . 0＜x＜2

答案解析收藏纠错 + 选题
9. (2020九上·大石桥月考) 如图是二次函数y＝ax²+bx+c图象的一部分，其对称轴是x＝﹣1，且过点（﹣3，0），说法：①abc＜0；②2a﹣b＝0；③﹣a+c＜0；④若（﹣5，y₁）、（ $\text{[math]}$ ，y₂）是抛物线上两点，则y₁＞y₂ ，其中说法正确的有（）个.

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2020九上·浉河期末) 在平面直角坐标系中，若干个半径为1的单位长度，圆心角为60°的扇形组成一条连续的曲线，点P从原点O出发，向右沿这条曲线做上下起伏运动（如图），点P在直线上运动的速度为每1个单位长度.点P在弧线上运动的速度为每秒 $\text{[math]}$ 个单位长度，则2019秒时，点P的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024九上·南阳期末) 方程 $\text{[math]}$ 的根是.

答案解析收藏纠错 + 选题
12. (2020九上·浉河期末) 如图，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到 $\text{[math]}$ ，这时点 $\text{[math]}$ 恰好在同一直线上，则 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题
13. (2020九上·浉河期末) 如图，点B是双曲线y＝ $\text{[math]}$ （k≠0）上的一点，点A在x轴上，且AB＝2，OB⊥AB，若∠BAO＝60°，则k＝.

答案解析收藏纠错 + 选题
14. (2020九上·浉河期末) 如图，在边长为2的正方形ABCD中，以点D为圆心，AD长为半径画 $\text{[math]}$ ，再以BC为直径画半圆，若阴影部分①的面积为S₁ ，阴影部分②的面积为S₂ ，则图中S₁﹣S₂的值为.（结果保留π）

答案解析收藏纠错 + 选题
15. (2020九上·浉河期末) 如图，在▱ABCD中，AB＝6，BC＝6 $\text{[math]}$ ，∠D＝30°，点E是AB边的中点，点F是BC边上一动点，将△BEF移沿直线EF折叠，得到△GEF ，当FG∥AC时，BF的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2020九上·浉河期末) 解下列方程：
1. （1） x²﹣2x﹣2=0；
2. （2）（x﹣1）（x﹣3）=8.
答案解析收藏纠错 + 选题
17. (2020九上·浉河期末) 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别是A（﹣4，1），B（﹣1，2），C（﹣2，4）.

（ 1 ）将△ABC向右平移4个单位后得到△A₁B₁C₁ ，请画出△A₁B₁C₁ ，并写出点B₁的坐标；

（ 2 ）△A₂B₂C₂和△A₁B₁C₁关于原点O中心对称，请画出△A₂B₂C₂ ，并写出点C₂的坐标；

（ 3 ）连接点A和点B₂ ，点B和点A₂ ，得到四边形AB₂A₂B，试判断四边形AB₂A₂B的形状（无须说明理由）.

答案解析收藏纠错 + 选题
18. (2020九上·浉河期末) 图①是一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字1，2，3，4，图②是一个正六边形棋盘，现通过掷骰子的方式玩跳棋游戏，规则是：将这枚骰子掷出后，看骰子向上三个面（除底面外）的数字之和是几，就从图②中的A点开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法跳动．
1. （1）随机掷一次骰子，则棋子跳动到点C处的概率是
2. （2）随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点C处的概率．
答案解析收藏纠错 + 选题
19. (2020九上·浉河期末) 如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点（点P不与A，B两点重合），连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP.
1. （1）求证：△BOQ≌△POQ；
2. （2）若直径AB的长为12.
  ①当PE＝时，四边形BOPQ为正方形；
  
  ②当PE＝时，四边形AEOP为菱形.
答案解析收藏纠错 + 选题

20. (2020九上·浉河期末) 参照学习函数的过程方法，探究函数 $\text{[math]}$ 的图象与性质，因为 $\text{[math]}$ ，即 $\text{[math]}$ ，所以我们对比函数 $\text{[math]}$ 来探究列表：

$\text{[math]}$	…	-4	-3	-2	-1	$\text{[math]}$	$\text{[math]}$	1	2	3	4	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	1	2	4	-4	-2	-1	$\text{[math]}$	$\text{[math]}$	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	2	3	5	-3	-2	0	$\text{[math]}$	$\text{[math]}$	…

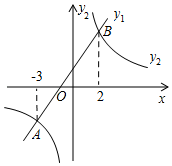
描点：在平面直角坐标系中以自变量 $\text{[math]}$ 的取值为横坐标，以 $\text{[math]}$ 相应的函数值为纵坐标，描出相应的点如图所示：

（1）请把 $\text{[math]}$ 轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；
（2）观察图象并分析表格，回答下列问题：
①当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而；（“增大”或“减小”）

② $\text{[math]}$ 的图象是由 $\text{[math]}$ 的图象向平移个单位而得到的；

③图象关于点中心对称.（填点的坐标）
（3）函数 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的面积.

答案解析收藏纠错 + 选题

21. (2021九上·平昌期中) 某水果商场经销一种高档水果，原价每千克50元，连续两次降价后每千克32元，若每每次下降的百分率相同．
1. （1）求每次下降的百分率；
2. （2）若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，且要尽快减少库存，那么每千克应涨价多少元？
答案解析收藏纠错 + 选题
22. (2020九上·浉河期末) 在Rt△ABC中，∠BCA＝90°，∠A＜∠ABC，D是AC边上一点，且DA＝DB，O是AB的中点，CE是△BCD的中线.
1. （1）如图a，连接OC，请直接写出∠OCE和∠OAC的数量关系：；
2. （2）点M是射线EC上的一个动点，将射线OM绕点O逆时针旋转得射线ON，使∠MON＝∠ADB，ON与射线CA交于点N.
  ①如图b，猜想并证明线段OM和线段ON之间的数量关系；
  
  ②若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段ME的长度(用含m的代数式表示).
答案解析收藏纠错 + 选题
23. (2020九上·浉河期末) 如图，若b是正数.直线l：y＝b与y轴交于点A，直线a：y＝x﹣b与y轴交于点B；抛物线L：y＝﹣x²+bx的顶点为C，且L与x轴右交点为D.
1. （1）若AB＝6，求b的值，并求此时L的对称轴与a的交点坐标；
2. （2）当点C在l下方时，求点C与l距离的最大值；
3. （3）设x₀≠0，点（x₀ ， y₁），（x₀ ， y₂），（x₀ ， y₃）分别在l，a和L上，且y₃是y₁ ， y₂的平均数，求点（x₀ ， 0）与点D间的距离；
4. （4）在L和a所围成的封闭图形的边界上，把横、纵坐标都是整数的点称为“美点”，分别直接写出b＝2019和b＝2019.5时“美点”的个数.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省信阳市浉河区2020届九年级上学期数学期末考试试卷

副标题：

*注意事项：

河南省信阳市浉河区2020届九年级上学期数学期末考试试卷

试题分析

总体分析

题量分析

难度分析

知识点分析