浙江省嘉兴市六校联盟2020-2021学年七年级上学期数学期...

更新时间：2024-07-13 浏览次数：195 类型：期中考试

一、选择题（本大题有10个小题，每小题3分，共30分）

1. (2022·珠海模拟) -5 的相反数是（）

A . -5 B . $\text{[math]}$ C . $\text{[math]}$ D . 5

答案解析收藏纠错 + 选题
2. (2020七上·嘉兴期中) 嘉兴市某天的最高气温为7℃，最低气温为-1℃，则这天嘉兴市的最高气温与最低气温的差为（）

A . 6℃ B . 7℃ C . 8℃ D . -8℃

答案解析收藏纠错 + 选题
3. (2020七上·嘉兴期中) “ $\text{[math]}$ 的2倍与 $\text{[math]}$ 的和”用代数式表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2020七上·嘉兴期中) 下列各组数中，相等的是（）

A . $\text{[math]}$ 与 $\text{[math]}$ B . $\text{[math]}$ 与 $\text{[math]}$ C . $\text{[math]}$ 与 $\text{[math]}$ D . $\text{[math]}$ 与 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020七上·嘉兴期中) 如图所示，在数轴上表示实数 $\text{[math]}$ 的点可能是（）

A . 点M B . 点N C . 点P D . 点Q

答案解析收藏纠错 + 选题
6. (2020七上·嘉兴期中) 单项式 $\text{[math]}$ 的次数和系数分别是（）

A . 2，-3 B . $\text{[math]}$ C . $\text{[math]}$ D . 3，-3

答案解析收藏纠错 + 选题
7. (2020七上·嘉兴期中) 若 $\text{[math]}$ ，则a与a的倒数的大小关系是（）

A . a大 B . a的倒数大 C . 一样大 D . 无法比较

答案解析收藏纠错 + 选题
8. (2020七上·嘉兴期中) 若一个正数的平方根是 $\text{[math]}$ 和 $\text{[math]}$ ， $\text{[math]}$ 的立方根是-2，则 $\text{[math]}$ 的算术平方根是（）

A . 0 B . 4 C . -4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020七上·嘉兴期中) 当x=1时， $\text{[math]}$ ，则x=-1时， $\text{[math]}$ 的值为（）

A . -3 B . -4 C . -5 D . -6

答案解析收藏纠错 + 选题
10. (2020七上·嘉兴期中) 我国古代《易经》一书中记载：远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”.如图所示，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数.由图可知，孩子自出生后的天数是（）

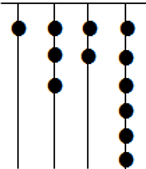
A . 84 B . 336 C . 510 D . 1326

答案解析收藏纠错 + 选题

二、填空题（本大题有10个小题，每小题3分，共30分）

11. (2020七上·嘉兴期中) 若向南走35米记作+35米，则向北走43米记作米.

答案解析收藏纠错 + 选题
12. (2020七上·嘉兴期中) 一周时间有604800秒，数604800用科学记数法表示为.

答案解析收藏纠错 + 选题
13. (2024七下·怀柔期末) 写出一个比 $\text{[math]}$ 大且比 $\text{[math]}$ 小的无理数：．

答案解析收藏纠错 + 选题
14. (2020七上·嘉兴期中) 若 $\text{[math]}$ 与 $\text{[math]}$ 是同类项，则x=.

答案解析收藏纠错 + 选题
15. (2020七上·嘉兴期中) 在数轴上，与表示-1的点距离3个单位长度的点表示的数为.

答案解析收藏纠错 + 选题
16. (2020七上·嘉兴期中) 通过计算可以得到： $\text{[math]}$
$\text{[math]}$ ，从这些数据可得 $\text{[math]}$ 精确到千分位的近似值是.

答案解析收藏纠错 + 选题
17. (2024七上·安定期末) 如果 $\text{[math]}$ ，那么 $\text{[math]}$ =.

答案解析收藏纠错 + 选题
18. (2020七上·嘉兴期中) 如图所示，以数轴的单位长度线段为边作一个正方形，以表示数 $\text{[math]}$ 的点为圆心，正方形的对角线长为半径画弧，交数轴于点A，则点A表示的数是.

答案解析收藏纠错 + 选题
19. (2020七上·嘉兴期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2020七上·嘉兴期中) 对于任何实数a，可用 $\text{[math]}$ 表示不超过a的最大整数，如 $\text{[math]}$ 现对72进行如下操作： $\text{[math]}$ ，这样对72只需进行3次操作后变为1，类似地：
1. （1）对64只需进行次操作后变为1.
2. （2）只需进行3次操作后变为1的所有正整数中，最大的是.
答案解析收藏纠错 + 选题

三、解答题（本大题有6个小题，第21~24题每小题6分，第25~26题每小题8分，共40分）

21. (2020七上·嘉兴期中) 计算
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
22. (2020七上·嘉兴期中) 把下列各数填写在相应的括号内（填写序号即可）.
① $\text{[math]}$ ，② $\text{[math]}$ ，③ $\text{[math]}$ ，④ $\text{[math]}$ ，⑤ $\text{[math]}$ ，⑥ $\text{[math]}$ ，⑦ $\text{[math]}$ ，

⑧ $\text{[math]}$ （两个1之间依次多一个0），⑨ $\text{[math]}$

整数｛                                      ｝

分数｛                                      ｝

无理数｛                                      ｝

答案解析收藏纠错 + 选题
23. (2020七上·嘉兴期中) 已知多项式 $\text{[math]}$ .
1. （1）求次数为3的项的系数和.
2. （2）当 $\text{[math]}$ 时，求该多项式的值.
答案解析收藏纠错 + 选题

24. (2020七上·嘉兴期中) 某仓库中有一种货物库存为250千克，现规定运入为正，运出为负，一天中七次出入情况如下表：

第一次	第二次	第三次	第四次	第五次	第六次	第七次
-30	+78	-17	+101	-98	+23	-33

（1）在第次记录时库存最多.
（2）最终这一天库存增加或减少了多少？
（3）若货物装卸费用为每千克0.4元，则这一天需装卸费用多少元？

答案解析收藏纠错 + 选题

25. (2020七上·嘉兴期中) 任意无理数都是由整数部分和小数部分构成的.
已知一个无理数 $\text{[math]}$ ，它的整数部分是 $\text{[math]}$ ，则它的小数部分可以表示为 $\text{[math]}$ .例如：

$\text{[math]}$ ，即 $\text{[math]}$ ，显然 $\text{[math]}$ 的整数部分是2，小数部分是 $\text{[math]}$ .

根据上面的材料，解决下列问题：
1. （1）若 $\text{[math]}$ 的整数部分是 $\text{[math]}$ ， $\text{[math]}$ 的整数部分是 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
2. （2）若 $\text{[math]}$ 的整数部分是 $\text{[math]}$ ，小数部分是 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
26. (2020七上·嘉兴期中) 某工厂生产一种茶几和茶具，茶几每套定价300元，茶具每套定价80元，厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套茶几送一套茶具；②茶几和茶具都按定价的90%付款．某客户要到该厂购买茶几10套，茶具x套（茶具超过10套）．
1. （1）若该客户按照方案①购买，需付款元（用含x的代数式表示）；
  按照方案②购买，需付款元（用含x的代数式表示）．
2. （2）若 $\text{[math]}$ ，通过计算说明此时按哪种方案购买较为合算．
3. （3）当 $\text{[math]}$ 时，你能给出一种更为合算的购买方案吗？若能，请写出你的购买方案．
答案解析收藏纠错 + 选题