甘肃省张掖市甘州区大成中学2020-2021学年九年级上学期...

更新时间：2021-02-26 浏览次数：318 类型：月考试卷

一、单选题

1. (2020九上·甘州月考) 下面如图所示的几何体的俯视图是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020九上·甘州月考) 下列函数中，是二次函数的是（　　）

A . y＝2x﹣1 B . y＝ $\text{[math]}$ C . y＝x²+1 D . y＝（x﹣1）²﹣x²

答案解析收藏纠错 + 选题
3. (2020九上·槐荫期末) 已知点（3，﹣4）在反比例函数 $\text{[math]}$ 的图象上，则下列各点也在该反比例函数图象上的是（）

A . （3，4） B . （﹣3，﹣4） C . （﹣2，6） D . （2，6）

答案解析收藏纠错 + 选题
4. (2020九上·甘州月考) 如果ab=cd，且abcd≠0，则下列比例式不正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·绿园模拟) 如图，有一斜坡 $\text{[math]}$ 的长 $\text{[math]}$ 米，坡角 $\text{[math]}$ ，则斜坡 $\text{[math]}$ 的铅垂高度 $\text{[math]}$ 为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·甘州月考) 已知点C是线段 $\text{[math]}$ 的黄金分割点，且 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020九上·甘州月考) 将抛物线y＝2x²先向右平移4个单位，再向上平移5个单位，得到的新抛物线的解析式为（　　）

A . y＝2（x+4）²+5 B . y＝2（x﹣4）²+5 C . y＝2（x+4）²﹣5 D . y＝2（x﹣4）²﹣5

答案解析收藏纠错 + 选题
8. (2020九上·甘州月考) 函数 $\text{[math]}$ 与y=-mx²+m(m≠0)在同一直角坐标系中的大致图象可能是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2020九上·甘州月考) 如图，在平行四边形ABCD中，∠B＝60°，将△ABC沿对角线AC折叠，点B的对应点落在点E处，且点B，A，E在一条直线上，CE交AD于点F，则图中等边三角形共有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
10. (2020九上·甘州月考) 对于抛物线y＝﹣（x﹣2）²+3，下列判断正确的是（　　）

A . 抛物线开口向上 B . 抛物线的顶点是（﹣2，3） C . 对称轴为直线x＝2 D . 它可由抛物线y＝﹣x² 向左平移2个单位再向上平移3个单位得到

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·甘州月考) 计算cos²45°+tan60°cos30°的值为．

答案解析收藏纠错 + 选题
12. (2020九上·甘州月考) 二次函数y＝x²+2的图象的顶点坐标是.

答案解析收藏纠错 + 选题
13. (2020九上·甘州月考) 已知△ABC∽△A′B′C′，相似比为3∶4，△ABC的周长为6，则△A′B′C′的周长为_.

答案解析收藏纠错 + 选题
14. (2020九上·甘州月考) 已知： $\text{[math]}$ ，且y≠4，那么 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
15. (2020九上·甘州月考) 如图，一辆小车沿着坡度为 $\text{[math]}$ 的斜坡从点A向上行驶了50米到点B处，则此时该小车离水平面的垂直高度为.

答案解析收藏纠错 + 选题
16. (2020九上·甘州月考) 已知点A（x₁ ， y₁）、B（x₂ ， y₂）在二次函数y＝（x﹣1）²+1的图象上，若0＞x₂＞x₁ ，则y₁y₂.（填“＞”、“＜”或“＝”）.

答案解析收藏纠错 + 选题
17. (2023九上·海门期中) 在一个不透明的袋子中有50个除颜色外均相同的小球，通过多次摸球试验后，发现摸到白球的频率约为36%，估计袋中白球有个.

答案解析收藏纠错 + 选题
18. (2020九上·甘州月考) 已知点A（x₁ ， y₁）、B（x₂ ， y₂）为二次函数 $\text{[math]}$ 图象上的两点，若 $\text{[math]}$ ，则y₁y₂.（填“＞”、“＜”或“＝”）

答案解析收藏纠错 + 选题

三、解答题

19. (2020九上·甘州月考) 如图为三个并列的边长相同的正方形，试说明：∠1+∠2+∠3＝90°.

答案解析收藏纠错 + 选题
20. (2020九上·甘州月考) 计算：
1. （1） 2cos²30°﹣2sin60°•cos45°；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2024·梅县区模拟) 如图，在△ABC中，AD是BC边上的高，AE是BC边上的中线，∠C=45°，sinB= $\text{[math]}$ ，AD=1．
1. （1）求BC的长；
2. （2）求tan∠DAE的值．
答案解析收藏纠错 + 选题
22. (2020九上·甘州月考) 如图，点O是平面直角坐标系的原点，点A、B、C的坐标分别是（1，-1）、（2，1）、（1，1）.
1. （1）作图：以点O为位似中心在y轴的左侧把原来的四边形OABC放大两倍（不要求写出
  作图过程）；
2. （2）直接写出点A、B、C对应点A’、B’、C’的坐标.
答案解析收藏纠错 + 选题

23. (2020九上·甘州月考) 如图，某数学活动小组要测量建筑物 $\text{[math]}$ 的高度，他们借助测角仪和皮尺进行了实地测量，测量结果如下表.

测量项目	测量数据
测角仪到地面的距离	$\text{[math]}$
点 $\text{[math]}$ 到建筑物的距离	$\text{[math]}$
从 $\text{[math]}$ 处观测建筑物顶部 $\text{[math]}$ 的仰角	$\text{[math]}$
从 $\text{[math]}$ 处观测建筑物底部 $\text{[math]}$ 的俯角	$\text{[math]}$

请根据需要，从上面表格中选择3个测量数据，并利用你选择的数据计算出建筑物 $\text{[math]}$ 的高度.（结果精确到0.1米，参考数据： $\text{[math]}$ . $\text{[math]}$ ）（选择一种方法解答即可）

答案解析收藏纠错 + 选题

24. (2020九上·甘州月考) 如图，一农户要建一个矩形猪舍，猪舍的一边利用现有的住房墙，另外三边用 25m 长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个小门.
1. （1）如果住房墙长 12 米，门宽为 1 米，所围矩形猪舍的长、宽分别为多少时，猪舍面积为 80m²？
2. （2）如果住房墙长 12 米，门宽为 1 米，当 AB 边长为多少时，猪舍的面积最大？最大面积是多少？
3. （3）如果住房墙足够长，门宽为a 米，设 AB＝x 米，当 6.5≤x≤7 时，猪舍的面积 S 先增大，后减小，直接写出a 的范围.
答案解析收藏纠错 + 选题
25. (2020九上·甘州月考) 已知函数 $\text{[math]}$ 是关于x的二次函数.求：
1. （1）满足条件的m的值；
2. （2） m为何值时，抛物线有最低点？求出这个最低点，这时当x为何值时，y随x的增大而增大？
3. （3） m为何值时，函数有最大值？最大值是多少？这时当x为何值时，y随x的增大而减小？
答案解析收藏纠错 + 选题
26. (2020九上·甘州月考) 已知y＝（m+1）x 是二次函数，且当x＞0时，y随x的增大而减小.
1. （1）求m的值；
2. （2）当自变量的值为多少时，函数有最值？最值是多少？
答案解析收藏纠错 + 选题
27. (2020九上·甘州月考) 如图，正方形DEFG的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，已知△ABC的边BC＝15，高AH＝10，求正方形DEFG的边长和面积.

答案解析收藏纠错 + 选题
28. (2020九上·甘州月考) 已知抛物线y＝a（x+4）²经过点M（﹣3，2），请解答下列问题：
1. （1）求抛物线的函数表达式，并说明此抛物线是由哪条抛物线经过平移得到的；
2. （2）求抛物线的开口方向，顶点坐标和对称轴；
3. （3）写出y随x的变化规律；
4. （4）求出函数的最大值或最小值.
答案解析收藏纠错 + 选题
29. (2020九上·甘州月考) 如图，一次函数y₁＝k₁x+2与反比例函数 $\text{[math]}$ 的图象交于点A（4，m）和B（﹣8，﹣2），与y轴交于点C.
1. （1）求一次函数与反比例函数的解析式；
2. （2）求当y₁＞y₂时，x的取值范围；
3. （3）过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E，当S_四边形_ODAC：S_△_ODE＝3：1时，求点P的坐标.
答案解析收藏纠错 + 选题
30. (2020九上·甘州月考)

图（1）图（2）图（3）

（操作发现）

如图①，在正方形ABCD中，点N、M分别在边BC、CD上，连结AM、AN、MN.

∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE.易证：△ANM≌△ANE，从而得DM+BN＝MN.
1. （1）（实践探究）
  在图（1）条件下，若CN＝3，CM＝4，则正方形ABCD的边长是.
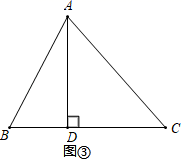
2. （2）如图（2），点M、N分别在边CD、AB上，且BN＝DM.点E、F分别在BM、DN上，∠EAF＝45°，连接EF，猜想三条线段EF、BE、DF之间满足的数量关系，并说明理由.
3. （3）（拓展）
  如图（3），在矩形ABCD中，AB＝3，AD＝4，点M、N分别在边DC、BC上，连结AM，AN，已知∠MAN＝45°，BN＝1，求DM的长.
答案解析收藏纠错 + 选题