黑龙江省佳木斯市桦南县2019-2020学年九年级下学期数学...

更新时间：2024-07-13 浏览次数：142 类型：期中考试

一、填空题

1. (2020九下·桦南期中) 国家统计局新闻发言人盛来运2010年7月15日在国新办的新闻发布会上宣布，据初步测算，上半年国内生产总值是172840亿元，比上年同期增长了3.7个百分点．数据172840亿元用科学记数法表示为亿元（结果保留三个有效数字）．

答案解析收藏纠错 + 选题
2. (2020九下·桦南期中) 在函数y＝ $\text{[math]}$ +（|x|+3）中，则x的取值范围是．

答案解析收藏纠错 + 选题
3. (2020九下·桦南期中) 如图，点D，E分别在线段AB、AC上，BE，CD相交于O，AB＝AC，要使△BDO≌△CEO，需要添加一个条件是．（填一个即可）

答案解析收藏纠错 + 选题
4. (2020九下·桦南期中) 一天晚上小明在家练抛球游戏，他在袋里（有红、黄、蓝、绿大小相同的四色球）随机一手抓两个球，则红、绿两球在一起的概率为．

答案解析收藏纠错 + 选题
5. (2020九下·桦南期中) 若关于x的一元一次不等式组 $\text{[math]}$ 的解集为x＞3，那么a的取值范围是．

答案解析收藏纠错 + 选题
6. (2020九下·桦南期中) 如图，将一块含 $\text{[math]}$ 角的直角三角板和半圆形量角器按如图的方式摆放，使三角板斜边与半圆相切，若半径 $\text{[math]}$ ，则图中阴影部分的面积是．（结果保留π）

答案解析收藏纠错 + 选题
7. (2020九下·桦南期中) 一个圆锥的表面积为40πcm² ，底面圆的半径是4cm，则圆锥侧面展开图的圆心角是度．

答案解析收藏纠错 + 选题
8. (2020九下·桦南期中) 如图，MN是⊙O的直径，MN=4，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，则PA+PB的最小值为．

答案解析收藏纠错 + 选题
9. (2020九下·桦南期中) 在矩形ABCD中，AB＝9cm，E是直线CD上一点，连接AC，BE，若AC与BE交于点F且DE＝3cm，则EF：BE的值是．

答案解析收藏纠错 + 选题
10. (2020九下·桦南期中)
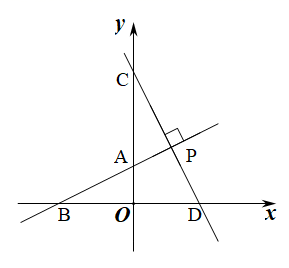
如图，在△ABC中，∠ACB=90°，∠A=60°，AC=a，作斜边AB边中线CD，得到第一个三角形ACD；DE⊥BC于点E，作Rt△BDE斜边DB上中线EF，得到第二个三角形DEF；依此作下去…则第n个三角形的面积等于．

答案解析收藏纠错 + 选题

二、单选题

11. (2020九下·桦南期中) 下列运算正确的是（）

A . x⁶÷x²＝x³ B . （2a³）²＝4a⁵ C . x²+x⁴＝x⁶ D . （﹣2a）²a＝4a³

答案解析收藏纠错 + 选题
12. (2023八上·新丰期中) 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
13. (2020九下·桦南期中) 如图是一个由多个相同小正方体搭成的几何体的俯视图，图中所标数字为该位置小正方体的个数，则这个几何体的主视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
14. (2020九下·桦南期中) 抚顺市中小学机器人科技大赛中，有7名学生参加决赛，他们决赛的成绩各不相同，其中一名参赛选手想知道自己能否进入前4名，他除了知道自己成绩外还要知道这7名学生成绩的（）

A . 中位数 B . 众数 C . 平均数 D . 方差

答案解析收藏纠错 + 选题
15. (2020九下·桦南期中) 某城市计划用两年时间增加全市绿化面积，若平均每年绿化面积比上一年增长20%，则两年后城市绿化面积是原来的（）

A . 1.2倍 B . 1.4倍 C . 1.44倍 D . 1.8倍

答案解析收藏纠错 + 选题
16. (2020七下·双阳期末) 如图，在平面直角坐标系中，边长为1的正方形ABCD中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
17. (2020九下·桦南期中) 已知关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 的解是非负数，那么 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021九上·讷河期中) 今年学校举行足球联赛，共赛17轮（即每队均需参赛17场），记分办法是：胜1场得3分，平1场得1分，负1场得0分．在这次足球比赛中，小虎足球队得16分，且踢平场数是所负场数的整数倍，则小虎足球队所负场数的情况有（　　）

A . 2种 B . 3种 C . 4种 D . 5种

答案解析收藏纠错 + 选题
19. (2020九下·桦南期中) 如图，Rt△ABC的顶点A在双曲线 $\text{[math]}$ 的图象上，直角边BC在x轴上，∠ABC=90°，∠ACB=30°，OC=4，连接OA，∠AOB=60°，则k的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
20. (2020九下·桦南期中)
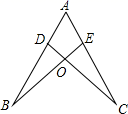
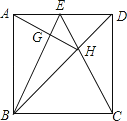
如图，正方形ABCD中，点E是AD边中点，BD、CE交于点H，BE、AH交于点G，则下列结论：
①AG⊥BE； ②BG=4GE； ③S_△_BHE=S_△_CHD； ④∠AHB=∠EHD．其中正确的个数是（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

三、解答题

21. (2021九上·抚远期中) 先化简（1+ $\text{[math]}$ ）÷ $\text{[math]}$ ，再从1、﹣1、0、2中选择一个合适的数代入并求值．

答案解析收藏纠错 + 选题
22. (2020九下·桦南期中) 如图，正方形网格中，每一个小正方形的边长都是1个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，1），B（3，2），C（2，4）．
1. （1）画出△ABC关于x轴对称的△A₁B₁C₁ ，直接写出点A₁的坐标；
2. （2）画出△ABC绕点O逆时针旋转90°后的△A₂B₂C₂；
3. （3）在（2）的条件下，求BC边所扫过的面积．（结果保留π）
答案解析收藏纠错 + 选题
23. (2020九下·桦南期中) 如图，抛物线y=x²+bx+c与x轴交于A（﹣1，0）和B（3，0）两点，交y轴于点E．
1. （1）求此抛物线的解析式．
2. （2）若直线y=x+1与抛物线交于A、D两点，与y轴交于点F，连接DE，求△DEF的面积．
答案解析收藏纠错 + 选题

24. (2020七上·太湖期末) 为了强化司机的交通安全意识，我市利用交通安全宣传月对司机进行了交通安全知识问卷调查．关于酒驾设计了如下调查问卷：

克服酒驾﹣﹣你认为哪种方式最好？（单选）

A加大宣传力度，增强司机的守法意识． B在汽车上张贴温馨提示：“请勿酒驾”．

C司机上岗前签“拒接酒驾”保证书． D加大检查力度，严厉打击酒驾．

E查出酒驾追究一同就餐人的连带责任．

随机抽取部分问卷，整理并制作了如下统计图：

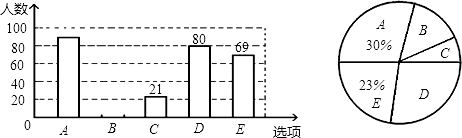
根据上述信息，解答下列问题：

（1）本次调查的样本容量是多少？
（2）补全条形图，并计算B选项所对应扇形圆心角的度数；
（3）若我市有3000名司机参与本次活动，则支持D选项的司机大约有多少人？

答案解析收藏纠错 + 选题

25. (2020九下·桦南期中) 小明和爸爸周末步行去游泳馆游泳，爸爸先出发了一段时间后小明才出发，途中小明在离家 $\text{[math]}$ 米处的报亭休息了一段时间后继续按原来的速度前往游泳馆．爸爸、小明离家的距离 $\text{[math]}$ （单位：米）， $\text{[math]}$ 单位：米）与小明所走时间 $\text{[math]}$ （单位：分钟）之间的函数关系如图所示，请结合图象信息解答下列问题：
1. （1）分别求出爸爸离家的距离 $\text{[math]}$ 和小明到达报亭前离家的距离 $\text{[math]}$ 与时间 $\text{[math]}$ 之间的函数关系式；
2. （2）求小明在报亭休息了多长时间遇到姗姗来迟的爸爸？
3. （3）若游泳馆离小明家 $\text{[math]}$ 米，请你通过计算说明谁先到达游泳馆？
答案解析收藏纠错 + 选题
26. (2020九下·桦南期中) 如图，在△ABC中，AB=BC，AD⊥BC于点D，BE⊥AC于点E，AD与BE交于点F，BH⊥AB于点B，点M是BC的中点，连接FM并延长交BH于点H．
1. （1）如图①所示，若∠ABC=30°，求证：DF+BH= $\text{[math]}$ BD；
2. （2）如图②所示，若∠ABC=45°，如图③所示，若∠ABC=60°（点M与点D重合），猜想线段DF、BH与BD之间又有怎样的数量关系？请直接写出你的猜想，不需证明.
答案解析收藏纠错 + 选题
27. (2020九下·桦南期中) 为了落实党中央提出的“惠民政策”，我市今年计划开发建设A、B两种户型的“廉租房”共40套．投入资金不超过200万元，又不低于198万元．开发建设办公室预算：一套A型“廉租房”的造价为5.2万元，一套B型“廉租房”的造价为4.8万元．
1. （1）请问有几种开发建设方案？
2. （2）哪种建设方案投入资金最少？最少资金是多少万元？
3. （3）在（2）的方案下，为了让更多的人享受到“惠民”政策，开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金．每套A户型“廉租房”的造价降低0.7万元，每套B户型“廉租房”的造价降低0.3万元，将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”，如果同时建设A、B两种户型，请你直接写出再次开发建设的方案．
答案解析收藏纠错 + 选题
28. (2020九下·桦南期中) 如图，直线AB与坐标轴分别交于点A、点B，且OA、OB的长分别为方程x²－6x+8=0的两个根（OA＜OB），点C在y轴上，且OA︰AC=2︰5，直线CD垂直于直线AB于点P，交x轴于点D．
1. （1）求出点A、点B的坐标.
2. （2）请求出直线CD的解析式.
3. （3）若点M为坐标平面内任意一点，在坐标平面内是否存在这样的点M，使以点B、P、D、M为顶点的四边形是平行四边形?若存在，请直接写出点M的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题