高考必做题07：光电综合

更新时间：2021-04-24 浏览次数：119 类型：三轮冲刺

一、解答题

1. (2019·江苏模拟) 2019年1月，中国散裂中子源加速器打靶束流功率超过50kW，技术水平达到世界前列，散裂中子源是由加速器提供高能质子轰击重金属靶而产生中子的装置，一能量为10⁹eV的质子打到汞、钨等重核后，导致重核不稳定而放出20～30个中子，大大提高了中子的产生效率。一个高能质子的动量为p₀ ，打到质量为M、原来静止的钨核内，形成瞬时的复合核，然后再散裂出若干中子，已知质子质量为m，普朗克常量为h。
①求复合核的速度v；

②设复合核释放的某个中子的动量为p，求此中子的物质波波长λ。

答案解析收藏纠错 + 选题
2. (2019·扬州模拟) 已知氢原子的基态能量为E₁（E₁<0），量子数为n的激发态的能量为 $\text{[math]}$ ．现有一群氢原子处于n=3的能级，在向低能级跃迁过程中，其中从n=2能级向n=1能级跃迁辐射出的光照射某金属的表面恰能发生光电效应，求：
①该金属的极限频率；

②能从该金属表面逸出的光电子的最大初动能．

答案解析收藏纠错 + 选题
3. (2019·南通模拟) 我国自行研制的一种大型激光器，能发出频率为ν、功率为P₀的高纯度和高亮度激光．如图所示，光电管的阴极K用某金属制成，闭合开关S，当该激光射向阴极，产生了光电流．移动变阻器的滑片P，当光电流恰为零时，电压表的示数为U_c ，已知普朗克常量为h，电子电荷量为e，真空中的光速为c．求：

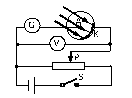
①激光器发出的光子的动量p；

②光电管阴极K的截止频率ν_c ．

答案解析收藏纠错 + 选题

二、综合题

4. (2021·唐山模拟) 如图所示为一研究导体棒在磁场中运动的装置。两平行光滑金属轨道倾角为30°，导轨间距d=1m。导轨上端通过单刀双掷开关可以分别与1、2相连，其中1连接光电管，2连接一个电容C=0.25F的电容器。两平行导轨间存在着垂直于轨道平面向上的匀强有界磁场，磁感应强度B=IT，磁场长度DE=1m。现利用光电管把光信号转换为电信号，A和K分别是光电管的阳极和阴极，电源电压为U。用发光功率为P的激光器发出频率为 $\text{[math]}$ 的光全部照射在K上，开关与1接通，回路中形成电流。已知阴极K材料的逸出功为W₀ ，普朗克常量为h，电子电荷量为e。初始时导体棒恰好能静止在磁场上边缘D处，导体棒垂直导轨放置，各处电阻均不计，重力加速度取10m/s²。求：
1. （1）光电子到达A时的最大动能E_km；（答案用字母表示）
2. （2）假设每个入射的光子会产生1个光电子，所有的光电子都能到达A，激光器发光功率P=13.26w， $\text{[math]}$ =6.4×10¹⁴Hz、H=6.63×10^-34J·S、e=1.6×10^-19C，求导体棒的质量m；
3. （3）把开关快速搬到位置2，导体棒向下运动起来，在运动过程中始终与导轨垂直，求导体棒运动到E处时的速度大小。
答案解析收藏纠错 + 选题
5. (2021·江苏模拟) 我国中微子探测实验利用光电管把光信号转换为电信号。如图所示，A和K分别是光电管的阳极和阴极，加在A、K之间的电压为U。现用发光功率为P的激光器发出频率为v的光全部照射在K上，回路中形成电流。已知阴极K材料的逸出功为W₀ ，普朗克常量为h，电子电荷量为e。
1. （1）求光电子到达A时的最大动能E_km；
2. （2）若每入射N个光子会产生1个光电子，所有的光电子都能到达A，求回路的电流强度I。
答案解析收藏纠错 + 选题
6. (2020·济南模拟) 图甲为利用光电管研究光电效应的电路图，其中光电管阴极K的材料是钾，钾的逸出功为 $\text{[math]}$ 。图乙为实验中用某一频率的光照射光电管时，测量得到的光电管伏安特性曲线，当 $\text{[math]}$ 时，光电流刚好截止。已知 $\text{[math]}$ 。求
1. （1）本次实验入射光的频率是多少？
2. （2）当 $\text{[math]}$ 时，光电子到达阳极A的最大动能是多少？
答案解析收藏纠错 + 选题
7. (2019·海淀模拟) 光子不仅具有能量，而且具有动量。照到物体表面的光子被物体吸收或被反射时都会对物体产生一定的压强，这就是“光压”。光压的产生机理与气体压强产生的机理类似：大量气体分子与器壁的频繁碰撞产生持续均匀的压力，器壁在单位面积上受到的压力表现为气体的压强。
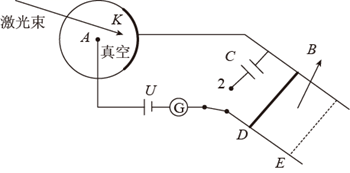
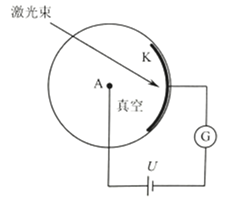
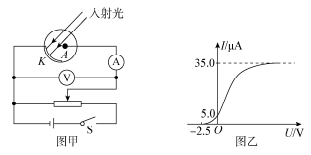
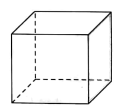
在体积为V的正方体密闭容器中有大量的光子，如图所示。为简化问题，我们做如下假定：每个光子的频率均为V，光子与器壁各面碰撞的机会均等，光子与器壁的碰撞为弹性碰撞，且碰撞前后瞬间光子动量方向都与器壁垂直；不考虑器壁发出光子和对光子的吸收，光子的总数保持不变，且单位体积内光子个数为n；光子之间无相互作用。已知：单个光子的能量s和动量p间存在关系ε=pc（其中c为光速），普朗克常量为h。
1. （1） ①写出单个光子的动量p的表达式（结果用c、h和ν表示）；
  ②求出光压I的表达式（结果用n、h和ν表示）；
2. （2）类比于理想气体，我们将题目中所述的大量光子的集合称为光子气体，把容器中所有光子的能量称为光子气体的内能.
  ①求出容器内光子气体内能U的表达式（结果用矿和光压，表示）；
  
  ②若体积为V的容器中存在分子质量为m、单位体积内气体分子个数为n'的理想气体，分子速率均为v，且与器壁各面碰撞的机会均等；与器壁碰撞前后瞬间，分子速度方向都与器壁垂直，且速率不变。求气体内能U'与体积V和压强p_气的关系；并从能量和动量之间关系的角度说明光子气体内能表达式与气体内能表达式不同的原因。
答案解析收藏纠错 + 选题
8. (2019·荆门模拟) 如图所示是使用光电管的原理图，当频率为 $\text{[math]}$ 的可见光照射到阴极K上时，电流表中有电流通过。
1. （1）当变阻器的滑动端P向滑动时（填“左”或“右”），通过电流表的电流将会增大。
2. （2）当电流表电流刚减小到零时，电压表的读数为U，则光电子的最大初动能为（已知电子电荷量为e）。
3. （3）如果不改变入射光的频率，而增加入射光的强度，则光电子的最大初动能将（填“增加”、“减小”或“不变”）。
答案解析收藏纠错 + 选题
9. (2019·朝阳模拟) 建立理想化的物理模型既是物理学的基本思想方法，也是物理学在应用中解决实际问题的重要途径。
1. （1）一段直导线，单位长度内有n个自由电子，电子电荷量为e。该导线通有电流时，自由电子定向移动的平均速率为v，求导线中的电流I。
2. （2）一水平放置的细水管，距地面的高度为h，有水从管口处以不变的速度源源不断地沿水平方向射出，水流稳定后落地的位置到管口的水平距离为 $\text{[math]}$ 。已知管口处水柱的横截面积为S，水的密度为ρ，重力加速度为g。水流在空中不散开，不计空气阻力。求：
  a．水从管口水平射出速度v₀的大小；
  
  b．水流稳定后，空中水的总质量m。
3. （3）现有一个点光源以功率P均匀地向各个方向发射波长为λ的光，如果每秒有n个光子射入人的瞳孔，就能引起人眼的视觉效应。已知人眼瞳孔的直径为d，普朗克常量为h，光在空气中速度为c，不计空气对光的吸收。求人眼能看到这个光源的最大距离L_m。
答案解析收藏纠错 + 选题
10. (2020·北京模拟) 光的干涉和衍射现象说明光具有波动性。爱因斯坦的光电效应理论和康普顿效应理论表明，光在某些方面确实也会表现得像是由一些粒子（即一个个有确定能量和动量的“光子”）组成的。人们意识到，光既具有波动性，又具有粒子性。（c为光速，h为普朗克常量）
1. （1）物理学家德布罗意把光的波粒二象性推广到实物例子，他提出假设：实物粒子也具有波动性，即每一个运动的粒子都与一个对应的波相联系，粒子的能量E和动量p跟它所对应波的频率v和波长λ之间也遵从如下关系： $\text{[math]}$ ， $\text{[math]}$ 。请依据上述关系以及光的波长公式，试推导单个光子的能量E和动量p间存在的关系；
2. （2）我们在磁场中学习过磁通量 $\text{[math]}$ ，其实在物理学中有很多通量的概念，比如电通量、光通量、辐射通量等等。辐射通量 $\text{[math]}$ 表示单位时间内通过某一截面的辐射能，其单位为 $\text{[math]}$ 。
  ①光子具有能量。一束波长为λ的光垂直照射在面积为S的黑色纸片上，其辐射通量为 $\text{[math]}$ ，且全部被黑纸片吸收，求该束光单位体积内的光子数n；
  
  ②光子具有动量。当光照射到物体表面上时，不论光被物体吸收还是被物体表面反射，光子的动量都会发生改变，因而对物体表面产生一种压力。求上一问中的光对黑纸片产生的压力大小，并判断若将黑纸片换成等大的白纸片，该束光对白纸片的压力有何变化。
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

高考必做题07：光电综合

副标题：

*注意事项：

高考必做题07：光电综合

物理考试

试题分析

总体分析

题量分析

难度分析

知识点分析