一、选择题:本题共12小题,每小题5分,共60分。
-
1.
已知集合

,则图中阴影部分的集合为( )
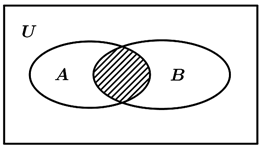
-
2.
已知

(其中i为虚数单位),则复数

( )
A .  B .
B .  C . 1
D . 2
C . 1
D . 2
-
3.
为了丰富教职工业余文化生活,某校计划在假期组织全体老师外出旅游,并给出了两个方案(方案一和方案二),每位老师均选择且只选择一种方案,其中有50%的男老师选择方案一,有75%的女老师选择方案二,且选择方案一的老师中女老师占40%,那么该校全体老师中女老师的比例为( )
-
4.
(2023高二上·广州期中)
果农采摘水果,采摘下来的水果会慢慢失去新鲜度.已知某种水果失去新鲜度h与其采摘后时间t(天)满足的函数关系式为

.若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果在多长时间后失去50%新鲜度(已知

,结果取整数)( )
A . 23天
B . 33天
C . 43天
D . 50天
-
5.
过椭圆内定点

且长度为整数的弦,称作该椭圆过点

的“好弦”.在椭圆

中,过点

的所有“好弦”的长度之和为( )
A . 120
B . 130
C . 240
D . 260
-
6.
已知

、

、

均为单位向量,且满足

,则

的值为( )
-
-
8.
某四棱锥的三视图如图所示,则该四棱锥的体积为( )

A . 2
B .  C .
C .  D . 4
D . 4
-
-
10.
设函数

,直线

是曲线

的切线,则a+b的最大值是( )
-
11.
坐标原点

且斜率为

的直线

与椭圆

交于

、

两点.若点

,则

面积的最大值为( )
-
二、填空题:本题共4小题,每小题5分,共20分。
-
-
14.

的展开式的常数项是
.
-
15.
已知四棱锥

的顶点均在球

的球面上,底面

是矩形,

,

,

,二面角

大小为120°,当

面积最大时,球

的表面积为
.
-
16.
已知

是奇函数,定义域为

,当

时,

(

),当函数

有3个零点时,则实数

的取值范围是
.
三、解答题:共70分。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
-
17.
已知数列

满足

-
(1)
证明:数列

是等差数列,并求数列

的通项公式;
-
-
18.
某学校共有1000名学生参加知识竞赛,其中男生400人,为了解该校学生在知识竞赛中的情况,采取分层抽样随机抽取了100名学生进行调查,分数分布在

分之间,根据调查的结果绘制的学生分数频率分布直方图如图所示:
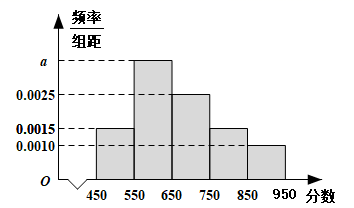
将分数不低于750分的学生称为“高分选手”.
(参考公式:  ,期中
,期中  )
)
|  | 0.15 | 0.10 | 0.005 | 0.025 | 0.010 | 0.005 | 0.001 |
|  | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
-
(1)
求

的值,并估计该校学生分数的平均数、中位数和众数(同一组中的数据用该组区间的中点值作代表);
-
(2)
现采用分层抽样的方式从分数落在

,

内的两组学生中抽取10人,再从这10人中随机抽取3人,记被抽取的3名学生中属于“高分选手”的学生人数为随机变量

,求

的分布列及数学期望;
-
(3)
若样本中属于“高分选手”的女生有10人,完成下列

列联表,并判断是否有97.5%的把握认为该校学生属于“高分选手”与“性别”有关?
| | 属于“高分选手” | 不属于“高分选手” | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
-
19.
如图,在五面体

中,面

为正方形,面

面

,

,

.
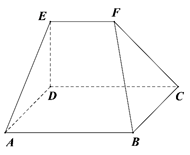
-
-
(2)
若

,

,求平面

与平面

所成的锐二面角的大小.
-
20.
已知椭圆

:

.左焦点

,点

在椭圆

外部,点

为椭圆

上一动点,且

的周长最大值为

.
-
(1)
求椭圆

的标准方程;
-
(2)
点

、

为椭圆

上关于原点对称的两个点,

为左顶点,若直线

、

分别与

轴交于

、

两点,试判断以

为直径的圆是否过定点.如果是请求出定点坐标,如果不过定点,请说明理由.
-
21.
已知函数

为

的导函数.
-
(1)
求函数

的极值;
-
(2)
设函数

,讨论

的单调性;
-
四、(二)选考题:共10分。请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。[选修4-4:坐标系与参数方程]
-
22.
(2022·河南模拟)
在直角坐标系

中,直线

的参数方程为

(

为参数),以坐标原点为极点,

轴的正半轴为极轴建立极坐标系,曲线

的极坐标方程为

-
(1)
求曲线

的直角坐标方程
-
(2)
已知点

的直角坐标为

,

与曲线

交于

两点,求

五、 [选修4-5:不等式选讲]
-
23.
已知函数

.
-
(1)
求不等式

的解集;
-

,期中
)