湘教版备考2021年中考数学三轮复习专题16 新定义和阅读理...

更新时间：2021-06-04 浏览次数：220 类型：三轮冲刺

一、单选题

1. (2019·株洲模拟) （2015永州）定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[﹣3.6]=﹣4．对于任意实数x ，下列式子中不正确的是（）

A . [x]=x（x为整数） B . 0≤x﹣[x]＜1 C . [x+y]≤[x]+[y] D . [n+x]=n+[x]（n为整数）

答案解析收藏纠错 + 选题
2. 若实数范围内定义一种运算“﹡”，使a*b=（a+1）²﹣ab，则方程（x+2）*5=0的解为（　　）

A . -2 B . ﹣2，3 C . $\text{[math]}$ , $\text{[math]}$ D . $\text{[math]}$ , $\text{[math]}$

答案解析收藏纠错 + 选题
3. 对于任意实数a、b，定义f（a，b）=a²+5a﹣b，如：f（2，3）=2²+5×2﹣3，若f（x，2）=4，则实数x的值是（　　）

A . 1或﹣6 B . ﹣1或6 C . ﹣5或1 D . 5或﹣1

答案解析收藏纠错 + 选题
4. 定义新运算：对于任意实数a，b，都有a⊕b=a²﹣3a+b，如3⊕5=3²﹣3×3+5，若x⊕1=11，则实数x的值（　　）

A . 2或﹣5 B . ﹣2或5 C . 2或5 D . ﹣2或﹣5

答案解析收藏纠错 + 选题
5. 定义运算：a⊗b=a（1﹣b）．下面给出了关于这种运算的几种结论：①2⊗（﹣2）=6，②a⊗b=b⊗a，③若a+b=0，则（a⊗a）+（b⊗b）=2ab，④若a⊗b=0，则a=0或b=1，其中结论正确的序号是（　　）

A . ①④ B . ①③ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题
6. 定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”如“967”就是一个“V数”．若十位上的数字为4，则从3，5，7，9中任选两数，能与4组成“V数”的概率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. 定义一种运算☆，其规则为a☆b= $\text{[math]}$ ，根据这个规则、计算2☆3的值是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . 5 D . 6

答案解析收藏纠错 + 选题

8. 先阅读下列表格：

x	…	1.1	1.2	1.3	1.4	…
x²+12x﹣15	…	﹣0.59	0.84	2.29	3.76	…

由表格可知方程x²+12x﹣15=0的正根的十分位是（　　）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题

9. 对于任意的正数m、n定义运算※为：m※n= $\text{[math]}$ ，计算（3※2）×（8※12）的结果为（　　）

A . 2﹣4 $\text{[math]}$ B . 2 C . 2 $\text{[math]}$ D . 20

答案解析收藏纠错 + 选题
10. (2016·岳阳) 对于实数a，b，我们定义符号max{a，b}的意义为：当a≥b时，max{a，b}=a；当a＜b时，max{a，b]=b，如：max{4，﹣2}=4，max{3，3}=3，若关于x的函数为y=max{x+3，﹣x+1}，则该函数的最小值是（　　）

A . 0 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
11. 对点（x，y）的一次操作变换记为p₁（x，y），定义其变换法则如下：p₁（x，y）=（x+y，x﹣y）；且规定P_n（x，y）=P₁（P_n_﹣₁（x，y））（n为大于1的整数）．例如：p₁（1，2）=（3，﹣1），p₂（1，2）=p₁（p₁（1，2））=p₁（3，﹣1）=（2，4），p₃（1，2）=p₁（p₂（1，2））=p₁（2，4）=（6，﹣2）．则p₂₀₁₄（1，﹣1）=（　　）

A . （0，2¹⁰⁰⁶） B . （2¹⁰⁰⁷ ， ﹣2¹⁰⁰⁷） C . （0，﹣2¹⁰⁰⁶） D . （2¹⁰⁰⁶ ， ﹣2¹⁰⁰⁶）

答案解析收藏纠错 + 选题

二、填空题

12. (2020九上·衡阳月考) 若对于实数 $\text{[math]}$ 定义一种新运算： $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2022七下·邕宁期末) 对于任意实数a、b，定义一种运算：a※b=ab﹣a+b﹣2．例如，2※5=2×5﹣2+5﹣2=ll．请根据上述的定义解决问题：若不等式3※x＜2，则不等式的正整数解是．

答案解析收藏纠错 + 选题
14. (2018九上·长沙期中) 对于实数a，b，定义运算“﹡”：a﹡b= $\text{[math]}$ ，例如4﹡2，因为4＞2，所以4﹡2=4²﹣4×2=8．若x₁ ， x₂是一元二次方程x²﹣5x+6=0的两个根，则x₁﹡x₂=．

答案解析收藏纠错 + 选题
15. 在实数范围内定义一种运算“*”，其规则为a*b=a²﹣b，根据这个规则，方程（x﹣1）*9=0的解为

答案解析收藏纠错 + 选题
16. (2020·常德) 阅读理解：对于x³﹣（n²+1）x+n这类特殊的代数式可以按下面的方法分解因式：
x³﹣（n²+1）x+n＝x³﹣n²x﹣x+n＝x（x²﹣n²）﹣（x﹣n）＝x（x﹣n）（x+n）﹣（x﹣n）＝（x﹣n）（x²+nx﹣1）．

理解运用：如果x³﹣（n²+1）x+n＝0，那么（x﹣n）（x²+nx﹣1）＝0，即有x﹣n＝0或x²+nx﹣1＝0，

因此，方程x﹣n＝0和x²+nx﹣1＝0的所有解就是方程x³﹣（n²+1）x+n＝0的解．

解决问题：求方程x³﹣5x+2＝0的解为．

答案解析收藏纠错 + 选题
17. (2022·衢州模拟) 阅读材料：设 $\text{[math]}$ ＝（x₁ ， y₁）， $\text{[math]}$ ＝（x₂ ， y₂），如果 $\text{[math]}$ ∥ $\text{[math]}$ ，则x₁•y₂＝x₂•y₁ ，根据该材料填空，已知 $\text{[math]}$ ＝（4，3）， $\text{[math]}$ ＝（8，m），且 $\text{[math]}$ ∥ $\text{[math]}$ ，则m＝.

答案解析收藏纠错 + 选题
18. (2017·湘潭) 阅读材料：设 $\text{[math]}$ =（x₁ ， y₁）， $\text{[math]}$ =（x₂ ， y₂）， $\text{[math]}$ ∥ $\text{[math]}$ ，则x₁•y₂=x₂•y₁ ．根据该材料填空：已知 $\text{[math]}$ =（2，3）， $\text{[math]}$ =（4，m），且 $\text{[math]}$ ∥ $\text{[math]}$ ，则m=．

答案解析收藏纠错 + 选题
19.
阅读下面材料：
如图，C是以点O为圆心，AB为直径的半圆上一点，且CO⊥AB，在OC两侧分别作矩形OGHI和正方形ODEF，且点I、F在OC上，点H、E在半圆上，求证：IG=FD．小云发现连接已知点得到两条线段，使可证明IG=FD．
请回答：小云所作的两条线段分别是和，证明IG=FD的依据是．

答案解析收藏纠错 + 选题
20. 阅读下列文字与例题将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．
例如：（1）　am　+an+　bm　+bn=（am+bm）+（an+bn）
=m（a+b）+n（a+b）
=（a+b）（m+n）
（2）x²﹣y²﹣2y﹣1=x²﹣（y²+2y+1）
=x²﹣（y+1）²
=（x+y+1）（x﹣y﹣1）
试用上述方法分解因式a²+2ab+ac+bc+b²= ．

答案解析收藏纠错 + 选题

三、解答题

21. 对a，b定义一种新运算M，规定M（a，b）= $\text{[math]}$ ，这里等式右边是通常的四则运算，例如：M（2，3）= $\text{[math]}$ =﹣12．
（1）如果M（2x，1）=M（1，﹣1），求实数x的值；
（2）若令y=M（x+ $\text{[math]}$ ， x﹣ $\text{[math]}$ ），则y是x的函数，当自变量x在﹣1≤x≤2的范围内取值时，函数值y为整数的个数记为k，求k的值．

答案解析收藏纠错 + 选题
22. 定义符号min{a，b}的含义为：当a≥b时，min{a，b}=b；当a＜b时，min{a，b}=a．如：min{1，﹣2}=﹣2，min{﹣1，2}=﹣1．
（1）求min{x²﹣1，﹣2}；
（2）已知min{x²﹣2x+k，﹣3}=﹣3，求实数k的取值范围；
（3）已知当﹣2≤x≤3时，min{x²﹣2x﹣15，m（x+1）}=x²﹣2x﹣15．直接写出实数m的取值范围．

答案解析收藏纠错 + 选题
23. 在平面直角坐标系xOy中，对于任意三点A，B，C的“矩面积”，给出如下定义：“水平底”a：任意两点横坐标差的最大值，“铅垂高”h：任意两点纵坐标差的最大值，则“矩面积”S=ah．例如：三点坐标分别为A（1，2），B（﹣3，1），C（2，﹣2），则“水平底”a=5，“铅垂高”h=4，“矩面积”S=ah=20．已知点A（1，2），B（﹣3，1），P（0，t）．
（1）若A，B，P三点的“矩面积”为12，求点P的坐标；
（2）直接写出A，B，P三点的“矩面积”的最小值．

答案解析收藏纠错 + 选题
24.
联想三角形内心的概念，我们可引入如下概念．
定义：到三角形的两边距离相等的点，叫做此三角形的准内心．
举例：如图1，若PD=PE，则点P为△ABC的准内心．
应用：如图2，BF为等边三角形的角平分线，准内心P在BF上，且PF= $\text{[math]}$ BP，求证：点P是△ABC的内心．
探究：已知△ABC为直角三角形，∠C=90°，准内心P在AC上，若PC= $\text{[math]}$ AP，求∠A的度数．

答案解析收藏纠错 + 选题
25.
阅读材料：如图，△ABC中，AB=AC，P为底边BC上任意一点，点P到两腰的距离分别为r₁ ， r₂ ，腰上的高为h，连接AP，则S_△_ABP+S_△_ACP=S_△_ABC ，即： $\text{[math]}$ AB•r₁+ $\text{[math]}$ AC•r₂= $\text{[math]}$ AB•h，∴r₁+r₂=h
1. （1）理解与应用
  如果把“等腰三角形”改成“等边三角形”，那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”，即：已知边长为2的等边△ABC内任意一点P到各边的距离分别为r₁ ， r₂ ， r₃ ，试证明：r₁+r₂+r₃= $\text{[math]}$ ．
2. （2）类比与推理
  边长为2的正方形内任意一点到各边的距离的和等于
3. （3）拓展与延伸
  若边长为2的正n边形A₁A₂…An内部任意一点P到各边的距离为r₁ ， r₂ ， …r_n ，请问r₁+r₂+…r_n是否为定值（用含n的式子表示），如果是，请合理猜测出这个定值．
答案解析收藏纠错 + 选题
26. 阅读材料，回答问题：材料：为解方程x⁴﹣x²﹣6=0，然后设x²=y，于是原方程可化为y²﹣y﹣6=0，解得y₁=﹣2，y₂=3．当y=﹣2时，x²=﹣2不合题意舍去；当y=3时，x²=3，解得x₁= $\text{[math]}$ ， x₂=﹣ $\text{[math]}$ ．故原方程的根为x₁= $\text{[math]}$ ， x₂=﹣ $\text{[math]}$ ．
请你参照材料给出的解题方法，解下列方程
①（x²﹣x）²﹣4（x²﹣x）﹣12=0．
② $\text{[math]}$ ﹣ $\text{[math]}$ =2．

答案解析收藏纠错 + 选题
27. 阅读下列材料，然后回答问题：
在进行二次根式运算时，我们有时会碰上如 $\text{[math]}$ 、 $\text{[math]}$ 这样的式子，其实我们还可以将其进一步化简： $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ；
$\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ -1．以上这种化简过程叫做分母有理化．
$\text{[math]}$ 还可以用以下方法化简： $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ -1．
（1）请用其中一种方法化简 $\text{[math]}$ ；
（2）化简： $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ +...+ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
28. 阅读探索：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）
（1）当已知矩形A的边长分别为6和1时，小亮同学是这样研究的：
设所求矩形的两边分别是x和y，由题意得方程组： $\text{[math]}$ ，消去y化简得：2x²﹣7x+6=0，
∵△=49﹣48＞0，∴x₁=?x₂=　?　，
∴满足要求的矩形B存在．
（2）如果已知矩形A的边长分别为2和1，请你仿照小亮的方法研究是否存在满足要求的矩形B．
（3）如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？

答案解析收藏纠错 + 选题
29.
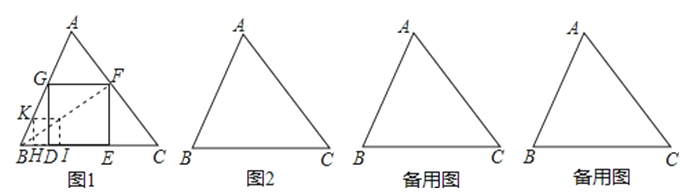
如图1，给定锐角三角形ABC，小明希望画正方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上，他发现直接画图比较困难，于是他先画了一个正方形HIJK，是的H，I，位于射线BC上，K位于射线BA上，而不需要求J必须位于AC上．这是他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG．
阅读以上材料，回答小明接下来研究的以下问题：
（1）如图2，给定锐角三角形ABC，画出所有长宽比为2：1的长方形DEFG，使D，E位于边BC上，F，G分别位于边AC，AB上．
（2）已知三角形ABC的面积为36，BC=12，在第（1）问的条件下，求长方形DEFG的面积．

答案解析收藏纠错 + 选题
30. 【阅读材料】已知，如图1，在面积为S的△ABC中，BC=a，AC=b，AB=c，内切圆O的半径为r，连接OA，OB，OC，△ABC被划分为三个小三角形．
∵S=S_△_OBC+S_△_OAC+S_△_OAB= $\text{[math]}$ BC•r+ $\text{[math]}$ AC•r+ $\text{[math]}$ AB•r= $\text{[math]}$ ar+ $\text{[math]}$ br+ $\text{[math]}$ cr= $\text{[math]}$ （a+b+c）r．
∴r= $\text{[math]}$ ．
（1）【类比推理】如图2，若面积为S的四边形ABCD存在内切圆（与各边都相切的圆），各边长分别为AB=a，BC=b，CD=c，AD=d，求四边形的内切圆半径r的值；
（2）【理解应用】如图3，在Rt△ABC中，内切圆O的半径为r，⊙O与△ABC各边分别相切于D、E和F，已知AD=3，BD=2，求r的值．

答案解析收藏纠错 + 选题
31. 阅读下列解答过程，并回答问题．
在（x²+ax+b）（2x²﹣3x﹣1）的积中，x³项的系数为﹣5，x²项的系数为﹣6，求a，b的值．
解：（x²+ax+b）•（2x²﹣3x﹣1）=
2x⁴﹣3x³+2ax³+3ax²﹣3bx=①
2x⁴﹣（3﹣2a）x³﹣（3a﹣2b）x²﹣3bx ②
根据对应项系数相等，有 $\text{[math]}$ 解得 $\text{[math]}$
回答：
（1）上述解答过程是否正确？　　．
（2）若不正确，从第　　步开始出现错误，其他步骤是否还有错误？　　．
（3）写出正确的解答过程．

答案解析收藏纠错 + 选题
32. 观察与思考：阅读下列材料，并解决后面的问题．
在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c，过A作 AD⊥BC于D(如图)，则sinB= $\text{[math]}$ ， sinC= $\text{[math]}$ ，即AD=csinB，AD=bsinC，于是csinB=bsinC，即 $\text{[math]}$ = $\text{[math]}$ .同理有： $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ = $\text{[math]}$ ，所以 $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$
即：在一个三角形中，各边和它所对角的正弦的比相等．在锐角三角形中，若已知三个元素（至少有一条边），运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料，完成下列各题.
（1）如图，△ABC中，∠B=45⁰ ， ∠C=75⁰ ， BC=60，则∠A= ；AC= ；
（2）如图，一货轮在C处测得灯塔A在货轮的北偏西30°的方向上，随后货轮以60海里／时的速度按北偏东30°的方向航行，半小时后到达B处，此时又测得灯塔A在货轮的北偏西75°的方向上(如图)，求此时货轮距灯塔A的距离AB.

答案解析收藏纠错 + 选题
33.
定义：如图，若双曲线 $\text{[math]}$ （k＞0）与它的其中一条对称轴y=x相交于两点A，B，则线段AB的长称为双曲线 $\text{[math]}$ （k＞0）的对径．

（1）求双曲线 $\text{[math]}$ 的对径；
（2）若某双曲线 $\text{[math]}$ （k＞0）的对径是 $\text{[math]}$ ．求k的值．

答案解析收藏纠错 + 选题
34. 平面直角坐标系xOy中，点A（x₁ ， y₁）与B（x₂ ， y₂），如果满足x₁+x₂=0，y₁﹣y₂=0，其中x₁≠x₂ ，则称点A与点B互为反等点．已知：点C（3，4）
1. （1）下列各点中，点C互为反等点；
  D（﹣3，﹣4），E（3，4），F（﹣3，4）
2. （2）已知点G（﹣5，4），连接线段CG，若在线段CG上存在两点P，Q互为反等点，求点P的横坐标x_P的取值范围；
3. （3）已知⊙O的半径为r，若⊙O与（2）中线段CG的两个交点互为反等点，求r的取值范围．
答案解析收藏纠错 + 选题