河北省衡水市景县2020-2021学年八年级下学期数学期末试...

更新时间：2021-07-30 浏览次数：127 类型：期末考试

一、选择题(本大题有16个小题，共42分．1~10小题各分，11~16 小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的)

1. (2023八下·东洲期末) 把 $\text{[math]}$ 化成最简二次根式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八上·卧龙月考) 下列命题中，逆命题是真命题的是（）

A . 直角三角形的两锐角互余 B . 对顶角相等 C . 若两直线垂直，则两直线有交点 D . 若 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九上·衡阳开学考) 某中学规定学生的学期体育成绩满分100分，其中课外体育占20%，期中考试成绩占30%，期末考试成绩占50%。小彤的三项成绩(百分制)依次为95，90，94，则小彤这学期的体育成绩为（）

A . 89 B . 90 C . 92 D . 93

答案解析收藏纠错 + 选题
4. (2021八下·景县期末) 矩形菱形、正方形都具有的性质（）

A . 对角线相等 B . 对角线互相平分 C . 对角线互相垂直 D . 对角线平分对角

答案解析收藏纠错 + 选题
5. (2021八下·景县期末) 在下列图象中，能作为一次函数y=-x+1的图象的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2021八下·景县期末) 已知函数y=(1-3m)x是正比例函数，且y随x的增大而增大，那么m的取值范围是（）

A . m> $\text{[math]}$ B . m< $\text{[math]}$ C . m>1 D . m<1

答案解析收藏纠错 + 选题
7. (2021八下·景县期末) 某校的校内有一个由两个相同的正六边形(即六条边都相等，六个角都相等)围成的花坛，边长为2.5m，如图中的阴影部分所示，校方想要将这个花坛在原有的基础上扩建成一个菱形区域如图所示，并在新扩、充的部分种上草坪，则扩建后菱形区域的周长为（）

A . 20m B . 25m C . 30m D . 35m

答案解析收藏纠错 + 选题
8. (2021八下·景县期末) 已知某一次函数的图象与直线y=-x+1平行，且过点(8，2)，那么此一次函数为（）

A . y=-x-2 B . y=-x+10 C . y=-x-6 D . y=-x-10

答案解析收藏纠错 + 选题
9. (2021八下·景县期末) 已知四边形ABCD是平行四边形，下列结论不正确的是（）

A . 当AC= BD时，它是菱形 B . 当AC⊥BD时，它是菱形 C . 当∠ABC=90°时，它是矩形 D . 当AB=BC时，它是菱形

答案解析收藏纠错 + 选题
10. (2021八下·景县期末) 如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≥ax+4的解集为（）

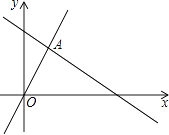
A . x≤3 B . x≥3 C . x≤ $\text{[math]}$ D . x≥ $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021八下·景县期末) 李大爷要围成一个矩形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边总长度恰好为24米。要围成的菜园是如图所示的长方形ABCD。设BC边的长为x米，AB边的长为y米，则y与x之间的函数关系式是（）

A . y=- $\text{[math]}$ x+12 B . y=-2x+24 C . y=2x-24 D . y= $\text{[math]}$ x-12

答案解析收藏纠错 + 选题
12. (2021八下·景县期末) A、B两地相距20千米，甲，乙两人都从A地去B地，图中I₁和l₂分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系，下列说法：①乙晚出发1小时；②乙出发3小时后追上甲；③甲的速度是4千米/小时；④乙先到达B地。其中正确的个数是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
13. (2021八下·景县期末) 如图，△AOB是等边三角形，B(2，0)，将△AOB绕O点逆时针方向旋转90°到△A'OB'位置，则A'坐标是（）

A . (-1， $\text{[math]}$ ) B . (- $\text{[math]}$ ，1) C . ( $\text{[math]}$ ，-1) D . (1，- $\text{[math]}$ )

答案解析收藏纠错 + 选题
14. (2021八下·景县期末) 如图1，在矩形MNPQ中，动点R从点N出发，沿若N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，OMNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（）

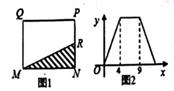
A . 当x=2时，y=5 B . 矩形MNPQ的面积是20 C . 当x=6时，y=10 D . 当y= $\text{[math]}$ 时，x=10

答案解析收藏纠错 + 选题
15. (2021八下·景县期末) 如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：
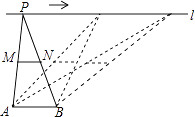
①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．
其中会随点P的移动而变化的是（）

A . ②③ B . ②⑤ C . ①③④ D . ④⑤

答案解析收藏纠错 + 选题
16. (2021八下·景县期末) 如图，在平面直角坐标系中，直线y=- $\text{[math]}$ x+3与矩形OABC的边AB、BC分别交于点E、F，若点B的坐标为(m，2)，则m的值可能为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题(本大题有3个小题，共12。17~18小题各3分；19小题有3个空，每空2分)

17. (2021八下·泗水期末) 已知一组数据10，8，9，x，5的众数是8，那么这组数据的方差是

答案解析收藏纠错 + 选题
18. (2021八下·景县期末) 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120 ，AB=1，则BC的长为

答案解析收藏纠错 + 选题
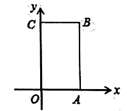
19. (2021八下·景县期末) 如图，长方形OABC中，0为平面直角坐标系的原点，A点的坐标为(4，0)，C点的坐标为(0，6)，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O→A→B→C→O的路线移动(即；沿着长方形移动一周)
1. （1）点B的坐标为
2. （2）当P点移动了4秒时，点P的坐标为
3. （3）在移动过程中，当点P到x轴距离为5个单位长度时，则点P移动的时间为
答案解析收藏纠错 + 选题

三、解答题(本大题7个小题，共66分解答应写出文字说明、证明过程或演算步骤)

20. (2021八下·景县期末) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
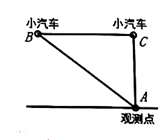
21. (2021八下·景县期末) “中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶的速度不得超过70km/h。如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到车速检测仪A处的正前方30m的C处，过了2s后；小汽车行驶到B处，测得小汽车与车速检测仪间的距离为50m，这辆小汽车超速了吗？

答案解析收藏纠错 + 选题
22. (2021八下·景县期末) 某校学生会向全校2900名学生发起了“爱心一日捐”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图1和图2，请根据相关信息，解答系列问题，
1. （1）本次接受随机抽样调查的学生人数为人，图1中m的值是
2. （2）求本次调查获取的样本数据的平均数、众数和中位数；
3. （3）根据样本数据，估计该校本次活动捐款金额不超过10元(包括10元)的学生人数。
答案解析收藏纠错 + 选题
23. (2021八下·景县期末) 如图，将 $\text{[math]}$ ABCD沿CE折叠，使点D落在BC边上的F处，点E在AD上。
1. （1）求证：四边形ABFE为平行四边形；
2. （2）若AB=4，BC=6，则四边形ABFE的周长为
答案解析收藏纠错 + 选题
24. (2021八下·景县期末) 某超市鸡蛋供应紧张，需每天从外地调运鸡蛋1200斤．超市决定从甲、乙两大型养殖场调运鸡蛋，已知甲养殖场每天最多可调出800斤，乙养殖场每天最多可调出900斤，从甲，乙两养殖场调运鸡蛋到该超市的路程和运费如下表：

到超市的路程(千米)

运费(元/斤·千米)

甲养殖场

200

0.012

乙养殖场

140

0.015

设从甲养殖场调运鸡蛋x斤，总运费为W元
1. （1）写出W与x的函数关系式；
2. （2）怎样安排调运方案才能使每天的总运费最省？
答案解析收藏纠错 + 选题
25. (2021八下·景县期末) 如图，在△ABC中，按如下步骤作图

①以点A为圆心，AB长为半径画弧

②以点C为圆心，CB长为半径画弧，两弧相交于点D

③连接BD，与AC交于点E，连接AD、CD
1. （1）求证：∠BAE=∠DAE；
2. （2）当AB=BC时，猜想四边形ABCD是什么四边形，并证明你的结论；
3. （3）当AC=8cm，BD=6cm，现将四边形ABCD通过割补，拼成一个正方形，那么这个正方形的边长是多少？
答案解析收藏纠错 + 选题
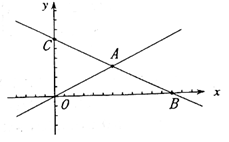
26. (2021八下·景县期末) 如图，在平面直角坐标系中，直线l₁：y=- $\text{[math]}$ +x+6分别与x轴、轴交于点B、C，且与直线l₂：y= $\text{[math]}$ x交于A。
1. （1）分别求出A、B、C的坐标；
2. （2）若D是线段OA上的点，且△COD的面积为l₂ ，求直线CD的函数表达式；
3. （3）在(2)的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由。
答案解析收藏纠错 + 选题