黑龙江省鹤岗市重点高中2020-2021学年高二下学期理数期...

更新时间：2021-07-29 浏览次数：87 类型：期末考试

一、选择题（本大题共有12个小题，每小题5分，共60分，在每小题给出的四选项中只有一项是符合题目要求的）

1. (2021高二下·鹤岗期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2021高二下·鹤岗期末) 已知 $\text{[math]}$ 是虚数单位，则复数 $\text{[math]}$ 的虚部为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021高二下·鹤岗期末) 下列函数中，是偶函数且值域为 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021高二下·鹤岗期末) 函数 $\text{[math]}$ 的大致图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2021高二下·鹤岗期末) 已知幂函数 $\text{[math]}$ 的图象过点 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 2 B . 3 C . 8 D . 9

答案解析收藏纠错 + 选题
6. (2021高二下·鹤岗期末) 已知 $\text{[math]}$ 是定义在 $\text{[math]}$ 上的周期为4的奇函数，若当 $\text{[math]}$ 时， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . -1 B . 0 C . 1 D . 2

答案解析收藏纠错 + 选题
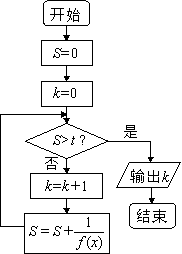
7. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ 的图象在 $\text{[math]}$ 处的切线与直线 $\text{[math]}$ 垂直。执行如图所示的程序框图，若输出的 $\text{[math]}$ 的值为 $\text{[math]}$ ，则判断框中 $\text{[math]}$ 的值可以为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ 为 $\text{[math]}$ 上的偶函数，对任意 $\text{[math]}$ ， $\text{[math]}$ ，均有 $\text{[math]}$
成立，若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021高二下·鹤岗期末) 曲线 $\text{[math]}$ 在 $\text{[math]}$ 处的切线与坐标轴围成的三角形面积为（）

A . e B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ ，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ ，若方程 $\text{[math]}$ 恰有4个不同的实数根，则实数 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2021高二下·鹤岗期末) 已知定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ 的导函数为 $\text{[math]}$ ，且满足 $\text{[math]}$ ，则关于 $\text{[math]}$ 不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共有4个小题，每小题5分，共20分）

13. (2021高二下·鹤岗期末) 若实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为.

答案解析收藏纠错 + 选题
14. (2021高二下·鹤岗期末) $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2021高二下·鹤岗期末) 设有下列四个命题：
$\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ ；

$\text{[math]}$ ：方程 $\text{[math]}$ 有两个不相等实根； $\text{[math]}$ ：函数 $\text{[math]}$ 的最小值是2．

则下述命题中所有真命题的序号是．

① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 恒成立，则实数 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题

三、解答题（本大题共有6个小题，共70分，第17题，10分，其余小题，每题12分。解答应写出文字说明、证明过程或演算步骤）

17. (2021高二下·鹤岗期末) 化简并求值：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时，求函数 $\text{[math]}$ 的值域；
2. （2）若函数 $\text{[math]}$ 在 $\text{[math]}$ 上的最大值为1，求实数 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
19. (2021高二下·鹤岗期末) 定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ 是单调函数，满足 $\text{[math]}$ ，且 $\text{[math]}$ ，（ $\text{[math]}$ ， $\text{[math]}$ ）．
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）判断 $\text{[math]}$ 的奇偶性，并证明；
3. （3）若对于任意 $\text{[math]}$ ，都有 $\text{[math]}$ 成立，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
20. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ 是奇函数， $\text{[math]}$ 是偶函数.
1. （1）求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
2. （2）设 $\text{[math]}$ ，若存在 $\text{[math]}$ ，使不等式 $\text{[math]}$ 成立，求实数 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
21. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ 的图象在 $\text{[math]}$ （ $\text{[math]}$ 为自然对数的底数）处的切线方程为 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 和 $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ 时， $\text{[math]}$ 恒成立，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题
22. (2021高二下·鹤岗期末) 已知函数 $\text{[math]}$ $\text{[math]}$
1. （1）讨论 $\text{[math]}$ 的单调性；
2. （2）若 $\text{[math]}$ 存在两个极值点 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值．
答案解析收藏纠错 + 选题