 B .
B .  C .
C .  D .
D . 
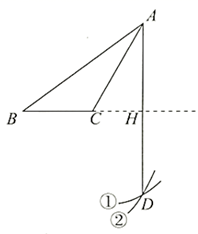
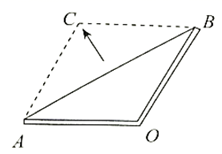
步骤1:以 为圆心,
长为半径画弧①;
步骤2:以 为圆心,
长为半径画弧②,交弧①于点
;
步骤3:连接 ,交
的延长线于点
.
则下列说法错误的是( )
已知 是一个正十二边形的外接圆,该正十二边形的半径为1,如果用它的面积来近似估计
的面积,则
的面积约是( )
| 我国魏晋时期著名数学家刘徽在“刻圆术”中提出:当正多边形的边数无限增加时,这个正多边形面积可无限接近它的外接圆面积,因此可以用正多边形的面积来进似估计这个圆的面积. |
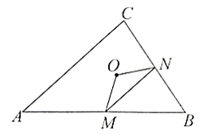
甲、乙、丙三人有如下判断:
甲: ;乙:四边形
的面积是定值;丙:当
时,
的周长取得最小值.则下列说法正确的是( )
| 甲:我的卡片上写着整式 乙:我用最简整式 |
根据以上信息,解决下列问题:

| 品种 | A | B | C | D | E |
| 购买数量/本 | 2 | 3 | 3 | 1 | 1 |
①选中调价后的售价不低于调价前售价的笔记本的概率为 ▲ .
②若小丽拿出的是一本C种笔记本,她还要从余下的四本中随机拿出两本,用树状图法或列表法求她选中B种笔记本的概率.
|
时间 |
3月 |
4月 |
||
|
型号 |
A |
B |
A |
B |
|
人数/人 |
25 |
20 |
20 |
10 |
|
加工个数 |
5400 |
4200 |
||
①直接写出抛物线 的对称轴和顶点坐标,并求
的长;
②当 时,求
的最大值和最小值的差.
①判断 与
是否相等,并说明理由;
②若 ,求
的长;