浙江省宁波市余姚市2020-2021学年八年级下学期数学期末...

更新时间：2024-07-13 浏览次数：281 类型：期末考试

一、选择题(每小题3分,共30分。)

1. (2023八下·鄞州期中) 下列四个生活安全警示图标，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021八下·余姚期末) 函数y＝ $\text{[math]}$ 中自变量x的取值范围是（）

A . x≥0 B . x＞2 C . x≠2 D . x≥2

答案解析收藏纠错 + 选题
3. (2021八下·余姚期末) 在▱ABCD中，∠A：∠B＝2：1，则∠C的度数为（）

A . 50° B . 60° C . 100° D . 120°

答案解析收藏纠错 + 选题
4. (2021八下·余姚期末) 用配方法解一元二次方程x²﹣4x﹣9＝0，变形正确的是（）

A . （x﹣2）²＝9 B . （x﹣2）²＝13 C . （x+2）²＝9 D . （x+2）²＝13

答案解析收藏纠错 + 选题
5. (2021八下·余姚期末) 应该是一组数据1，1，1，3，4，7，12，若加入一个整数a，一定不会发生变化的统计量为（）

A . 众数 B . 平均数 C . 中位数 D . 方差

答案解析收藏纠错 + 选题
6. (2022八下·义乌月考) 下列说法正确的是（）

A . 对角线互相垂直的四边形是菱形 B . 对角线互相垂直且相等的四边形是正方形 C . 一组对边平行另一组对边相等的四边形是平行四边形 D . 对角线相等的平行四边形是矩形

答案解析收藏纠错 + 选题
7. (2021八下·余姚期末) 如图，矩形内两个相邻正方形的面积分别为9和3，则阴影部分的面积为（）

A . 8﹣3 $\text{[math]}$ B . 9﹣3 $\text{[math]}$ C . 3 $\text{[math]}$ ﹣3 D . 3 $\text{[math]}$ ﹣2

答案解析收藏纠错 + 选题
8. (2021八下·余姚期末) 已知a ， b是实数，定义：a※b＝ab+a+b ．若m是常数x※（mx）＝﹣1，下列说法正确的是（）

A . 方程一定有实数根 B . 当m取某些值时，方程没有实数根 C . 方程一定有两个实数根 D . 方程一定有两个不相等的实数根

答案解析收藏纠错 + 选题
9. (2021八下·余姚期末) 如图，在平面直角坐标系xOy中，△AOB的顶点B在x轴正半轴上，AO＝AB ， P ， Q分别是OA ， AB的中点，函数y＝ $\text{[math]}$ （k＞0，x＞0）的图象过点P ，若S_△_OPQ＝3，则k的值为（）

A . 1.5 B . 2 C . 3 D . 6

答案解析收藏纠错 + 选题
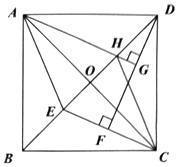
10. (2021八下·余姚期末) 如图，正方形ABCD中，AC ， E为线段BO上一动点（不包括O ， B两点），DF⊥CE于点F ，过点A作AG⊥DF于点G，交BD于点H ，连结AE ，则下列结论：①∠ADG＝∠DCF；②DG＝EF ， ③存在点E，使得EF＝GF；④四边形AECH是菱形．其中正确的结论有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题(每小题4分,共24分)

11. (2024八下·番禺期末) 计算： $\text{[math]}$ ＝．

答案解析收藏纠错 + 选题
12. (2021八下·余姚期末) 用反证法证明：“在△ABC中，若AB≠AC ，则∠B≠∠C”，则应假设．

答案解析收藏纠错 + 选题
13. (2021八下·余姚期末) 某种商品原价每件售价为400元，经过连续两次降价后，每件售价为288元，设平均每次降价的百分率为x，则可列方程为．

答案解析收藏纠错 + 选题
14. (2021八下·余姚期末) 如图，在矩形ABCD中，AB＝8，AD=6，将矩形沿EF翻折，使点C与点A重合，点B落在B'处，折痕与DC ， AB分别交于点E ， F ，则DE的长为．

答案解析收藏纠错 + 选题
15. (2021八下·余姚期末) 在平面直角坐标系中，我们把横坐标、纵坐标都是整数的点称为“整点”，已知点A ， B在反比例函数 $\text{[math]}$ 的图象上，若点A ， B都是整点，点O是坐标原点，且△ABO是等腰三角形，则AB的长为．

答案解析收藏纠错 + 选题
16. (2021八下·余姚期末) 如图，在▱ABCD中，AE⊥BC于点E ， M是AB的中点，已知S_△_ABD＝6，BC＝4，则MN的长为．

答案解析收藏纠错 + 选题

三、解答题(第17、18、19题各6分,第20、21题各8分,第22、23题各10分,第24题12分,共66分)

17. (2021八下·余姚期末) 计算：
1. （1） $\text{[math]}$ × $\text{[math]}$ + $\text{[math]}$ ；
2. （2）（ $\text{[math]}$ ﹣1）²+（ $\text{[math]}$ +2）（ $\text{[math]}$ ﹣2）．
答案解析收藏纠错 + 选题
18. (2021八下·余姚期末) 解方程：
1. （1）（2x﹣1）²＝16；
2. （2） 2x²+8x﹣1＝0．
答案解析收藏纠错 + 选题
19. (2021八下·余姚期末) 我们把小正方形的顶点叫做格点，每个顶点都在格点的四边形叫做格点四边形．如图，在所给的8×6方格纸中，B均为格点，请画出符合要求的格点四边形．
1. （1）在图1中画出一个以AB为边的矩形；
2. （2）在图2中画出一个以AB为对角线的菱形.
答案解析收藏纠错 + 选题
20. (2021八下·余姚期末) 已知反比例函数y＝ $\text{[math]}$ （k≠0）的图象经过点A（2，﹣3）．
1. （1）求函数表达式；
2. （2）当x＝﹣4时，求函数y的值；
3. （3）当x≤1且x≠0时，直接写出y的取值范围．
答案解析收藏纠错 + 选题

21. (2021八下·余姚期末) 甲、乙两名学生参加数学素质测试（有四项），每项测试成绩（单位：分）采用百分制

学生	数与代数	空间与图形	统计与概率	综合与实践	平均成绩	众数	中位数	方差
甲	95	90	a	85	x	b	90	12.5
乙	90	c	80	95	x	95	d	37.5

（1）根据表中信息判断哪个学生数学素质测试成绩更稳定？请说明理由．
（2）表格中的数据a＝；b＝；c＝；d＝；
（3）若数学素质测试的四个项目的重要程度有所不同，而给予“数与代数”、“空间与图形”、“统计与概率”、“综合与实践”四个项目在综合成绩中所占的比例分别为40%，30%，20%．计算得到乙的综合成绩为91.5分，请你计算甲的综合成绩

答案解析收藏纠错 + 选题

22. (2021八下·余姚期末) 如图，在▱ABCD中，E ， F分别是AB ，且AE＝CF ， DE ， H ．
1. （1）求证DE∥BF；
2. （2）求证：AG＝CH ．
答案解析收藏纠错 + 选题
23. (2021八下·余姚期末) 杨梅是我市特产水果之一，素有“初疑一颗值千金”之美誉!某杨梅园的杨梅除了直接销售到市区外，还可以让市民去园区采摘．已知杨梅在市区和园区的销售价格分别是10元/千克和15元/千克，该杨梅园今年六月第一周一共销售1000千克，销售收入12000元．
1. （1）该杨梅园今年六月第一周市区和园区分别销售了多少千克杨梅？
2. （2）为了促销，该杨梅园决定六月第二周将市区和园区销售价格均降低a（a＞0）元，预计市区和园区的销量将分别比第一周增加20a%和50%，设销售总额为w元，求w关于a的函数表达式；（不需要写出a的取值范围）
3. （3）在（2）的条件下，若预计该杨梅园第二周销售收入为14520元，求a的值.
答案解析收藏纠错 + 选题
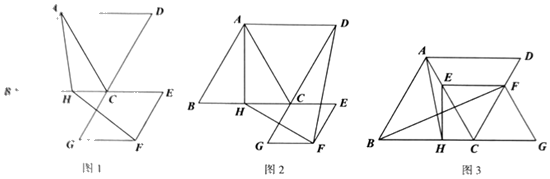
24. (2021八下·余姚期末) 如图1，四边形ABCD和四边形CEFG都是菱形，其中点E在BC的延长线上，点H在BC边上，连结AC ， HF ．已知AB＝2，∠ABC＝60°
1. （1）求证：△ABH≌△HEF；
2. （2）如图2，当H为BC中点时，连结DF；求DF的长。
3. （3）如图3，将菱形CEFG绕点C逆时针旋转120°，使点E在AC上，点G在BC的延长线上，连结EH ，请求出BF的长.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省宁波市余姚市2020-2021学年八年级下学期数学期末...

副标题：

*注意事项：

浙江省宁波市余姚市2020-2021学年八年级下学期数学期末...

试题分析

总体分析

题量分析

难度分析

知识点分析