浙江省宁波市鄞州2023年八年级下学期期中联考数学试卷

更新时间：2024-07-13 浏览次数：152 类型：期中考试

一、选择题(每小题3分，共30分)

1. (2023八下·鄞州期中) 下列四个生活安全警示图标，其中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八下·鄞州期中) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·奉化期末) 用反证法证明命题：“在△ABC中，∠A，∠B的对边分别是a，b，若∠A<∠B，则a<b．”时第一步应假设（）

A . a>b B . a≥b C . a≤b D . a≠b

答案解析收藏纠错 + 选题
4. (2024八下·凉州期末) 一组数据2，2，2，3，5，8，13，若加入一个数a，一定不会发生变化的统计量是（）

A . 方差 B . 平均数 C . 中位数 D . 众数

答案解析收藏纠错 + 选题
5. (2023八下·鄞州期中) 若关于x的一元二次方程x²+2x-k=0没有实数根，则实数k的取值范围为（）

A . k<-1 B . k≤-1 C . k≥-1 D . k>-1

答案解析收藏纠错 + 选题
6. (2023八下·鄞州期中) 某商品经过连续两次降价，价格从100元降为64元．已知两次降价的百分率都是x，则x满足的方程是（）

A . 64(1-2x)=100 B . 100(1-x)²=64 C . 64(1-x)²=100 D . 100(1-2x)=64

答案解析收藏纠错 + 选题
7. (2023八下·鄞州期中) 如图，大坝横截面的迎水坡AB的坡比为1：2，即BC：AC=1：2，若坡面AB长度10米，则坡面AB的水平宽度AC长为（）

A . $\text{[math]}$ B . 5 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023九上·滕州开学考) 如图，菱形ABCD的顶点A；B分别在y轴正半轴，x轴正半轴上，点C的横坐标为10，点D的纵坐标为8，若直线AC平行x轴，则菱形ABCD的边长值为（）

A . 9 B . $\text{[math]}$ C . 6 D . 3

答案解析收藏纠错 + 选题
9. (2023八下·鄞州期中) 从一块腰长为10cm的等腰直角三角形铁皮零料。上裁出一块面积为24cm²的矩形铁皮，要求矩形的四个顶点都在三角形的边上．若裁出的矩形全等视为同种裁法，则有几种不同的裁法？（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
10. (2024八下·北仑期中) 如图，点E是矩形ABCD内一点，连结AE，DE，AC，EC，BE，知道下列哪个选项的值就能要求△AEC的面积（）

A . △ABE与△BEC面积之差 B . △ADE与△BEC面积之差 C . △DEC与△BEC面积之差 D . △ADC与△DEC面积之差

答案解析收藏纠错 + 选题

二、填空题(每小题3分，共18分)

11. (2023八下·鄞州期中) 化简： $\text{[math]}$ =

答案解析收藏纠错 + 选题
12. (2023八下·鄞州期中) 已知一组数据是-1，0，-1，2，则这组数据的方差是

答案解析收藏纠错 + 选题
13. (2023八下·鄞州期中) 若m是方程3x²-x-2=0的一个根，则代数式6m²-2m的值为

答案解析收藏纠错 + 选题
14. (2023八下·鄞州期中) 如图，在四边形ABCD中，∠A+∠C=136°，点E在边AD上，连结BE，若∠D与∠EBC互补，则∠EBA的值为

答案解析收藏纠错 + 选题
15. (2023八下·鄞州期中) 如图，用长为a米的铝合金制成如图窗框，已知矩形AGHD，矩形BFEG，矩形EFCH的面积均相等，设AD的长为b米，则AB的长是米．(用含a，b的代数式表示)

答案解析收藏纠错 + 选题
16. (2023八下·鄞州期中) 如图，在凸四边形ABCD中，AB=4，AD=2 $\text{[math]}$ ， CD=2，∠BAD=45°，连结AC，取AC中点E，连结BE，则BE的最小值是

答案解析收藏纠错 + 选题

三、解答题(第17~19题各6分，第20~22 题各8分，第23 题10分，共52分)

17. (2023八下·鄞州期中)
1. （1）计算：
  $\text{[math]}$
2. （2）解方程：(x+3)²-4=0
答案解析收藏纠错 + 选题
18. (2023八下·鄞州期中) 图1是由边长为1的正方形构成的6x5的网格图，线段AB的端点都在格点上．
1. （1）在图1中画出一个以AB为一边，面积为12的矩形ABCD，并直接写出矩形ABCD对角线的长为 .
2. （2）命题“一组对边相等且有一个内角是直角的四边形是矩形”是真命题还是假命题？如果是假命题，请在图2中画一个顶点都是格点的凸四边形说明；若是真命题，请进行证明．
答案解析收藏纠错 + 选题
19. (2023八下·鄞州期中) 某公司需招聘一名员工，对应聘者A、B、C从笔试、面试、体能三个方面进行最化考核．A、B、C各项得分如下表：

笔试
面试
体能
A
82
79
91
B
84
80
76
C
81
90
72
1. （1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序；
2. （2）该公司规定：笔试、面试、体能得分分别不得低于80分、80 分、70分，并按60%，30%，10%的比例计入总分，总分最高者将被录用，根据规定，请你说明谁将被录用．
答案解析收藏纠错 + 选题
20. (2023八下·鄞州期中) 商场某种商品平均每天可售出30件，每件盈利50元．为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价1元，商场平均每天可多售出2件．设每件商品降价x元．据此规律，请回答：
1. （1）商场日销售增加件，每件商品盈利元；
2. （2）在上述条件不变，销售情况正常情况下，当每件商品降价多少元时，商场日盈利可达2100元？
答案解析收藏纠错 + 选题
21. (2023八下·鄞州期中) 如图，在矩形ABCD中，点E，F分别在AD，BC上，且AE=CF．
1. （1）求证：四边形BFDE是平行四边形：
2. （2）若AB=2，AD=4，四边形BFDE是菱形，求AE长．
答案解析收藏纠错 + 选题
22. (2023八下·鄞州期中) 我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．
例如：已知x可取任何实数，试求二次三项式x²+2x+3的最小值．

解：x²+2x+3=x²+2x+1+2=(x+1)²+2

∵无论x取何实数，都有(x+1)²≥0，

∴(x+1)²+2≥2，即x²+2x+3的最小值为2．
1. （1） [尝试应用]请直接写出2x²+4x+10的最小值；
2. （2） [拓展应用]试说明：无论x取何实数，二次根式 $\text{[math]}$ 4都有意义；
3. （3） [创新应用]如图，在四边形．ABCD中，AC⊥BD，若AC+BD=10，求四边形ABCD的面积最大值．
答案解析收藏纠错 + 选题
23. (2023八下·鄞州期中) 如图，在边长为4的正方形ABCD中，点E在边AD上，DE=1，连结BE，点P，点F分别是线段BE，边CD上的动点．
1. （1）连结AP，PF，若A，P，F三点共线，且AF=BE．
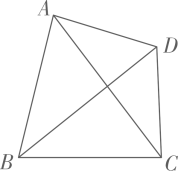
  ①求证：BE⊥AF；
  ②求PF的长；
2. （2）如图2，若CF=1，∠EPF=45°，则PF的长为.
3. （3）问题：“如图3，若CF=1，直线PF刚好平分正方形ABCD的面积，求PF的长．”在解决这一问题时，小红想先找到对应的点P，然后再求PF的长．经过不断的思考探索后，小红尝试以B为原点，建立坐标系来解决这一问题．
  请你帮助小红用无刻度的直尺在图3中找到点P，并直接写出PF的长为.
答案解析收藏纠错 + 选题