重庆市南川区2020-2021学年八年级下学期数学期末考试试...

更新时间：2024-07-13 浏览次数：165 类型：期末考试

一、单选题

1. (2021八下·南川期末) 二次根式 $\text{[math]}$ 有意义，则实数x的取值范围是（）

A . x＞2 B . x≥2 C . x≥﹣2 D . x≤﹣2

答案解析收藏纠错 + 选题
2. (2021八下·南川期末) 正比例函数y＝3x的图象必经过点（）

A . （﹣1，﹣3） B . （﹣1，3） C . （1，﹣3） D . （3，1）

答案解析收藏纠错 + 选题
3. (2021八下·南开期中) 下列各曲线中不能表示y是x的函数的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024八下·柳州期中) 若甲、乙、丙、丁四人参加跳远比赛，经过几轮初赛，他们的平均成绩相同，方差分别是：S $\text{[math]}$ ＝0.34，S $\text{[math]}$ ＝0.21，S $\text{[math]}$ ＝0.4，S $\text{[math]}$ ＝0.45.你认为最应该派去的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
5. (2023八上·北碚期末) 下列四个选项中，不符合直线y＝x﹣2的性质特征的选项是（）

A . 经过第一、三、四象限 B . y随x的增大而增大 C . 与x轴交于（﹣2，0） D . 与y轴交于（0，-2）

答案解析收藏纠错 + 选题
6. (2021八下·南川期末) 如图，小红在作线段AB的垂直平分线时，操作如下：分别以点A、B为圆心，大于 $\text{[math]}$ AB的长为半径、在线段AB的两侧画弧，两弧分别相交于点C、D，则直线CD即为所求，连接AC、BC、AD、BD，根据她的作法可知四边形ADBC一定是（）

A . 菱形 B . 矩形 C . 正方形 D . 梯形

答案解析收藏纠错 + 选题
7. (2023八上·蕉岭期中) 放学以后，红红和晓晓从学校分手，分别沿东南方向和西南方向回家，若红红和晓晓行走的速度都是50米/分，红红用12分钟到家，晓晓用16分钟到家，红红家和晓晓家的直线距离为（）

A . 600米 B . 800米 C . 1000米 D . 不能确定

答案解析收藏纠错 + 选题
8. (2021八下·南川期末) 如图，将一个矩形纸片ABCD折叠，使C点与A点重合.折痕为EF.若AB＝8，BC＝16，则BE的长是（）

A . 12 B . 10 C . 8 D . 6

答案解析收藏纠错 + 选题
9. (2021八下·南川期末) 如图，已知四边形ABCD是平行四边形，下列结论中正确的是（）

A . 当AC＝BD时，它是正方形 B . 当AC⊥BD时，它是矩形 C . 当∠ABC＝90°时，它是菱形 D . 当AB＝BC时，它是菱形

答案解析收藏纠错 + 选题
10. (2021八下·南川期末) 如图，正方形ABCD的边长为4.对角线AC，BD交于点O，E是AC延长线上一点，且CE＝CO.则BE的长度为（）

A . 4 $\text{[math]}$ B . 6 $\text{[math]}$ C . 2 $\text{[math]}$ D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2021八下·南川期末) 如图，A.B两地之间的路程为6000米，甲、乙两人骑车都从A地出发，已知甲先出发5分钟后，乙才出发，乙在A、B之间的C地追赶上甲，当乙追赶上甲后，乙立即返回A地，甲继续往B地前行.甲到达B地后停止骑行，乙骑行到达A地时也停止（乙在C地掉头时间忽略不计）.在整个骑行过程中，甲和乙都保持各自速度匀速骑行，甲乙两人相距的路程y（米）与甲出发的时间x（分钟）之间的关系如图所示.下列说法正确的是（）
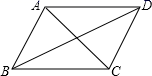
①乙的速度为227.5米/分；②甲的速度为150米/分；③图中M点的坐标为（21，2940）；④乙到达A地时，甲与B地相距3060米.（）

A . ①②③ B . ②③④ C . ①③④ D . ①②④

答案解析收藏纠错 + 选题
12. (2021八下·南川期末) 已知整数a.使得关于x的分式方程 $\text{[math]}$ +3＝ $\text{[math]}$ 有整数解.且关于x的一次函数y＝（a﹣1）x+6﹣a的图象不经过第四象限，则所有满足条件的整数a的值的和是（）

A . 10 B . 14 C . 16 D . 24

答案解析收藏纠错 + 选题

二、填空题

13. (2024八下·定州期末) 计算：（ $\text{[math]}$ ）²=

答案解析收藏纠错 + 选题
14. (2021八下·南川期末) 如图，在△ABC中，点D、E分别是AB、AC边的中点，若BC＝6cm.则线段DE＝cm.

答案解析收藏纠错 + 选题
15. (2021八下·南川期末) 矩形两条对角线的夹角为60°，对角线长为14，则该矩形较短边的边长为.

答案解析收藏纠错 + 选题
16. (2021八下·南川期末) 若点A（x₁ ， y₁）和点B（x₁+1，y₂）都在一次函数y＝2021x﹣2020的图象上，则y₁y₂（选择“＞”、“＜“或“＝”填空）.

答案解析收藏纠错 + 选题
17. (2021八下·南川期末) 如图，在Rt△ABC中，∠BCA＝90°.BC＝5.AC＝10，E为斜边AB边上的一动点，以EA、EC为边作平行四边形，则线段ED长度的最小值为.

答案解析收藏纠错 + 选题
18. (2021八下·南川期末) 为了改善城市绿化，南川区政府决定圈出一块地打造一片花园，花园中种植牡丹花、樱花、梅花供市民欣赏，经过一段时间，花园中已种植的牡丹花、樱花、梅花的面积之比为5：4：6，根据市民喜爱程度，将在花园余下空地继续种植这三种花，经过测算，需将余下空地面积的 $\text{[math]}$ 种植梅花，则梅花种植的总面积将达到这三种花种植总面积的 $\text{[math]}$ ，为了使牡丹花种植总面积与樱花种植总面积之比达到4：5，则花园内种植樱花的总面积与种植梅花的总面积之比 .

答案解析收藏纠错 + 选题

三、解答题

19. (2021八下·南川期末) 计算：
1. （1）（4+ $\text{[math]}$ ）（4﹣ $\text{[math]}$ ）；
2. （2） $\text{[math]}$ ﹣ $\text{[math]}$ × $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2021八下·南川期末) 如图，在平行四边形ABCD中，∠C＝50°.
1. （1）作∠BAD的平分线AE交DC于E；（尺规作图，不写作法，保留作图痕迹，并标明字母）.
2. （2）按（1）作图所示，若BC＝7，AB＝11，求CE的长.
答案解析收藏纠错 + 选题

21. (2021八下·南川期末) 某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）.相关数据整理如下：

八年级抽取的学生的竞赛成绩：4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10.

七，八年级抽取的学生的竞赛成绩统计表

年级	七年级	八年级
平均数	7.4	7.4
中位数	a	b
众数	7	c
合格率	85%	90%

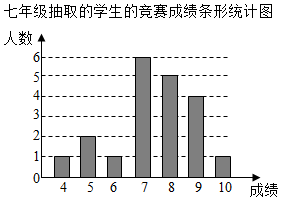
根据以上值息，解答下列问题：

（1）填空a＝；b＝；c＝.
（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；
（3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生整体成绩谁更优异.

答案解析收藏纠错 + 选题

22. (2021八下·南川期末) 已知：一次函数y＝kx+b的图象经过M（0，6），N（﹣2，2）两点.
1. （1）求一次函数的解析式；
2. （2）若点P（a﹣5，3a）在该函数图象上，求点P的坐标.
答案解析收藏纠错 + 选题
23. (2021八下·南川期末) 山王坪的门票销售分两类：一类为散客门票，价格50元/张，另一类为团体门票（一次性购买门票10张及以上），每张门票价格在散客价格基础上打8折.某班部分同学要去山王坪旅游，设参加旅游x人，购买门票需要y元.
1. （1）求y与x之间的函数解析式，并写出自变量的取值范围.
2. （2）请根据人数变化设计一种比较省钱的购票方案.
答案解析收藏纠错 + 选题
24. (2021八下·南川期末) 阅读理解：若x满足（30﹣x）（x﹣10）＝160，求（30﹣x ）²+（x﹣10）²的值.
解：设30﹣x＝a，x﹣10＝b，

则（30﹣x）（x﹣10）＝ab＝160，a+b＝（30﹣x）+（x﹣10）＝20，（30﹣x）²+（x﹣10）²＝a²+b²＝（a+b）²﹣2ab＝20²﹣2×160＝80

解决问题：
1. （1）若x满足（2020﹣x）（x﹣2016）＝4.求（2020﹣x） ²+（x﹣2016）²的值；
2. （2）如图，在矩形ABCD中，AB＝20，BC＝12，点E、F是BC、CD上的点，且BE＝DF＝x.分别以FC、CE为边在矩形ABCD外侧作正方形CFGH和CEMN，若矩形CEPF的面积为160平方单位，求图中阴影部分的面积和.
答案解析收藏纠错 + 选题
25. (2021八下·南川期末) 如图，在平行四边形ABCD中，点O是对角线AC的中点，点E是BC上一点，且AB＝AE，连接EO并延长交AD于点F.过点B作AE的垂线，垂足为H，交AC于点G.
1. （1）若AH＝6，HE＝2，求△ABE的面积；
2. （2）若∠ACB＝45°，求证：CG＝ $\text{[math]}$ DF.
答案解析收藏纠错 + 选题
26. (2021八下·南川期末) 已知﹣次函数y＝﹣ $\text{[math]}$ x+3的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E.
1. （1）求点E坐标.
2. （2）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积.
答案解析收藏纠错 + 选题