

 B .
B .  C .
C . 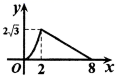 D .
D . 


|
A |
B |
C |
D |
|
漫步世园会 |
爱家乡,爱园艺 |
清新园艺之旅 |
车览之旅 |
小美和小红都计划去世园会游玩,她们各自在这4条路线中任意选择一条,每条线路被选择的可能性相同.
|
x |
0 |
1 |
2 |
3 |
4 |
|
y |
m |
0 |
1 |
0 |
﹣3 |

假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
①求证:a<0;
②若点A,P,Q三点到直线l:y=− x+
的距离相等,求线段PQ长.