山东省日照市五莲县2020-2021学年八年级上学期期末数学...

更新时间：2021-11-24 浏览次数：118 类型：期末考试

一、单选题

1. (2020八上·五莲期末) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020八上·五莲期末) 在下列图形中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2020八上·五莲期末) 若等腰三角形的两边长分别为3和7，则这个三角形的周长为（）

A . 13 B . 17 C . 13或17 D . 15或17

答案解析收藏纠错 + 选题
4. (2020八上·五莲期末) $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．（）

A . 1 B . 1.5 C . 2 D . 2.5

答案解析收藏纠错 + 选题
5. (2020八上·五莲期末) 一个多边形的内角和是外角和的3倍，则这个多边形是（　　）

A . 六边形 B . 七边形 C . 八边形 D . 九边形

答案解析收藏纠错 + 选题
6. (2022七下·卢龙期末) 如果多项式 $\text{[math]}$ 是一个完全平方式，则m的值是（）

A . ±4 B . 4 C . 8 D . ± 8

答案解析收藏纠错 + 选题
7. (2020八上·五莲期末) 下列约分结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020八上·五莲期末) 已知关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 的解是非负数，那么 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020八上·五莲期末) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，添加下列条件仍不能判定 $\text{[math]}$ 的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021八下·合浦期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，直线MN垂直平分AB交AB于M，交BC于N，且 $\text{[math]}$ ， $\text{[math]}$ ，则BN的长为（）

A . 4cm B . 3.5cm C . 3cm D . 4.5cm

答案解析收藏纠错 + 选题
11. (2020八上·五莲期末) 如图，等腰 $\text{[math]}$ 的底边BC长为4cm，面积为 $\text{[math]}$ ，腰AC的垂直平分线EF交AC于点E，交AB于点F，D为BC的中点，M为直线EF上的动点．则 $\text{[math]}$ 周长的最小值为（）

A . 6cm B . 8cm C . 9cm D . 10cm

答案解析收藏纠错 + 选题
12. (2020八上·五莲期末) 如图，D为△ABC边BC上一点，AB=AC，且BF=CD，CE=BD，则∠EDF等于（）

A . 90°－∠A B . 90°－ $\text{[math]}$ ∠A C . 180°－∠A D . 45°－ $\text{[math]}$ ∠A

答案解析收藏纠错 + 选题

二、填空题

13. (2020八上·五莲期末) 要使分式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
14. (2020八上·五莲期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
15. (2020八上·五莲期末) 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. (2021八上·东台月考) 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 连接AC，BD交于点M，连接OM，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 平分 $\text{[math]}$ ；④ $\text{[math]}$ .正确的结论序号是．

答案解析收藏纠错 + 选题

三、解答题

17. (2020八上·五莲期末)
1. （1）因式分解
  ① $\text{[math]}$
  
  ② $\text{[math]}$
2. （2）先化简，再求值：
  $\text{[math]}$ 其中 $\text{[math]}$ 且 $\text{[math]}$ 为整数，请从 $\text{[math]}$ 的以上范围中选一合适的数代入求值．
答案解析收藏纠错 + 选题
18. (2020八上·五莲期末) 如图，平面直角坐标系中 $\text{[math]}$ 的顶点均在格点上，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ．
1. （1）请在图中作出与 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称的 $\text{[math]}$ ；
2. （2）写出点 $\text{[math]}$ 和点 $\text{[math]}$ 的坐标．
3. （3）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
19. (2020八上·五莲期末) 甲乙两人加工同一种零件，甲每天加工的数量是乙每天加工数量的1.5倍．两人各加工900个这种零件，甲比乙少用5天．
1. （1）求甲、乙两人每天各加工多少个这样的零件．
2. （2）已知甲、乙两人加工这种零件每天的加工费分别是150元和120元，现有3000个这样的零件加工任务，甲单独加工一段时间后另有安排，剩余任务由乙单独完成．如果总加工费不超过5400元，那么甲至少加工了多少天？
答案解析收藏纠错 + 选题
20. (2024·寻乌模拟) 在等边三角形ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ．
1. （1）求证：△ABP≌△ACQ；
2. （2）请判断△APQ是什么形状的三角形？试说明你的结论．
答案解析收藏纠错 + 选题
21. (2020八上·五莲期末) 已知，如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点E是线段AD上一点，且 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）判断直线BE与AC的位置关系并证明．
答案解析收藏纠错 + 选题
22. (2020八上·五莲期末) 如图
1. （1）方法呈现：
  如图①：在 $\text{[math]}$ 中，若 $\text{[math]}$ ， $\text{[math]}$ ，点D为BC边的中点，求BC边上的中线AD的取值范围．
  
  解决此问题可以用如下方法：延长AD到点E使 $\text{[math]}$ ，再连接BE，可证 $\text{[math]}$ ，从而把AB、AC， $\text{[math]}$ 集中在 $\text{[math]}$ 中，利用三角形三边的关系即可判断中线AD的取值范围是，这种解决问题的方法我们称为倍长中线法；
2. （2）探究应用：
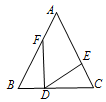
  如图②，在 $\text{[math]}$ 中，点D是BC的中点， $\text{[math]}$ 于点D，DE交AB于点E，DF交AC于点F，连接EF，判断 $\text{[math]}$ 与EF的大小关系并证明；
3. （3）问题拓展：
  如图③，在四边形ABCD中， $\text{[math]}$ ，AF与DC的延长线交于点F、点E是BC的中点，若AE是 $\text{[math]}$ 的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．
答案解析收藏纠错 + 选题