山东省德州市庆云县2020-2021学年九年级上学期期末数学...

更新时间：2021-12-09 浏览次数：124 类型：期末考试

一、单选题

1. (2020九上·庆云期末) 下列图形中，不是中心对称图形的是（）

A . 圆 B . 菱形 C . 正十边形 D . 等边三角形

答案解析收藏纠错 + 选题
2. (2020九上·庆云期末) 下列说法正确的是（）

A . “买一张电影票，座号是5的倍数”是必然事件 B . 了解全国快递包裹产生的包装垃圾数量适合采用全面调查（普查）方式 C . “明天降雨的概率为50%”，意味着明天一定有半天都在降雨 D . 一组数据的方差越小，则这组数据的波动也越小

答案解析收藏纠错 + 选题

3. (2024九下·宣化模拟) 验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表．根据表中数据，可得y关于x的函数表达式为（）

近视眼镜的度数y（度）	200	250	400	500	1000
镜片焦距x（米）	0.50	0.40	0.25	0.20	0.10

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

4. (2023九上·乐清月考) 已知二次函数 $\text{[math]}$ ，关于该函数在﹣1≤x≤3的取值范围内，下列说法正确的是（）

A . 有最大值﹣1，有最小值﹣2 B . 有最大值0，有最小值﹣1 C . 有最大值7，有最小值﹣1 D . 有最大值7，有最小值﹣2

答案解析收藏纠错 + 选题
5. (2021九上·南雄期末) 如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙ $\text{[math]}$ 交于点D，连结OD．若 $\text{[math]}$ ，则∠AOD的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·庆云期末) 一次函数y＝ax+b与反比列函数y＝ $\text{[math]}$ 的图象如图所示，则二次函数y＝ax²+bx+c的大致图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2020九上·庆云期末) 如图，在△ABC中，∠CAB＝55°，∠ABC＝25°，在同一平面内，将△ABC绕A点逆时针旋转70°得到△ADE，连接EC，则tan∠DEC的值（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·庆云期末) 一次会议上，每两个参加会议的人都相互握了一次手，有人统计一共握了45次手，这次会议到会的人数有多少人（）．

A . 8 B . 9 C . 10 D . 12

答案解析收藏纠错 + 选题
9. (2020九上·庆云期末) 如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，点A(10，0)，sin∠COA= $\text{[math]}$ .若反比例函数 $\text{[math]}$ 经过点C，则k的值等于（）

A . 10 B . 24 C . 48 D . 50.

答案解析收藏纠错 + 选题
10. (2020九上·庆云期末) 如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C移动至终点C，设P点经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
11. (2020九上·庆云期末) 如图，AB是垂直于水平面的建筑物．为测量AB的高度，小红从建筑物底端B点出发，沿水平方向行走了52米到达点C，然后沿斜坡CD前进，到达坡顶D点处， $\text{[math]}$ ．在点D处放置测角仪，测角仪支架DE高度为0.8米，在E点处测得建筑物顶端A点的仰角 $\text{[math]}$ 为 $\text{[math]}$ （点A，B，C，D，E在同一平面内）．斜坡CD的坡度（或坡比） $\text{[math]}$ ，那么建筑物AB的高度约为（）
（参考数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

A . 65.8米 B . 71.8米 C . 73.8米 D . 119.8米

答案解析收藏纠错 + 选题
12. (2020九上·庆云期末) 如图，抛物线y＝－x²＋2x＋m＋1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．
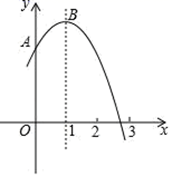
①抛物线y＝－x²＋2x＋m＋1与直线y＝m＋2有且只有一个交点；②若点M（－2，y₁）、点N（ $\text{[math]}$ ，y₂）、点P（2，y₃）在该函数图象上，则y₁<y₂<y₃；③将该抛物线向左平移2个单位，再向下平移2个单位，所得抛物线解析式为y＝－（x＋1）²＋m；④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为 $\text{[math]}$ ．其中正确的判断有（）

A . ①②③④ B . ②③④ C . ①③④ D . ①③

答案解析收藏纠错 + 选题

二、填空题

13. (2020九上·庆云期末) 如果关于x的一元二次方程x²﹣4x+k=0有实数根，那么k的取值范围是.

答案解析收藏纠错 + 选题
14. (2024九下·武侯月考) 一枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数.连续掷两次骰子，在骰子向上的一面上，第二次出现的点数是第一次出现的点数的2倍的概率是.

答案解析收藏纠错 + 选题
15. (2020九上·庆云期末) 若点A（﹣3，y₁），B（﹣2，y₂），C（1，y₃）都在反比例函数y＝﹣ $\text{[math]}$ 的图象上，则y₁ ， y₂ ， y₃按照从小到大的顺序排列是

答案解析收藏纠错 + 选题
16. (2020九上·庆云期末) 如图，四边形ABCD是矩形， $\text{[math]}$ ， $\text{[math]}$ ，以点A为圆心，AB长为半径画弧，交CD于点E，交AD的延长线于点F，则图中阴影部分的面积是.

答案解析收藏纠错 + 选题
17. (2020九上·庆云期末) 如图，在⊙O中，弦AB=1，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为．

答案解析收藏纠错 + 选题
18. (2020九上·庆云期末) 如图，在Rt△ABC中，∠ABC＝90°，BC＝3，D为斜边AC的中点，连接BD，点F是BC边上的动点（不与点B、C重合），过点B作BE⊥BD交DF延长线交于点E，连接CE，下列结论：①若BF＝CF，则CE²+AD²＝DE²；②若∠BDE＝∠BAC，AB＝4，则CE＝ $\text{[math]}$ ；③△ABD和△CBE一定相似；④若∠A＝30°，∠BCE＝90°，则DE＝ $\text{[math]}$ ．其中正确的是．（填写所有正确结论的序号）

答案解析收藏纠错 + 选题

三、解答题

19. (2020九上·庆云期末) 计算：
1. （1） 2sin60°tan30°+cos²30°-tan45°．
2. （2）（2x﹣3）²﹣2（2x﹣3）﹣3＝0．
答案解析收藏纠错 + 选题
20. (2020九上·庆云期末) 如图所示，在平面直角坐标系中，△ABC的三个顶点分别是A（﹣2，﹣2）、B（﹣4，﹣1）、C（﹣4，﹣4）．

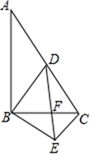
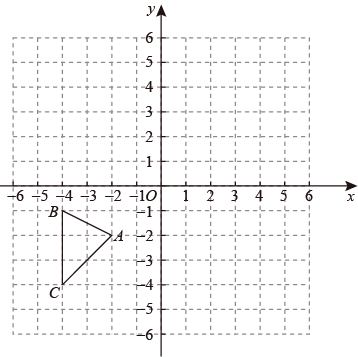
⑴画出△ABC关于原点O成中心对称的△A₁B₁C₁；

⑵画出△ABC绕点O逆时针旋转90度的△A₂B₂C₂；

⑶在x轴上找到一点P，使PA+PB的和最小值，求出P点坐标及最小值．

答案解析收藏纠错 + 选题
21. (2020九上·庆云期末) 为了预防“甲型H₁N₁”，某学校对教室采用药薰消毒法进行消毒，已知药物燃烧时，室内每立方米空气中的含药量y（mg）与时间x（min）成正比例，药物燃烧后，y与x成反比例，如图所示，现测得药物8min燃毕，此时室内空气每立方米的含药量为6mg，请你根据题中提供的信息，解答下列问题：
1. （1）药物燃烧时，求y关于x的函数关系式？自变量x的取值范围是什么？药物燃烧后y与x的函数关系式呢？
2. （2）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能杀灭空气中的毒，那么这次消毒是否有效？为什么？
答案解析收藏纠错 + 选题
22. (2022·开鲁模拟) 如图，△ABC内接于⊙O，AB是⊙O的直径，AC＝CE，连接AE交BC于点D，延长DC至F点，使CF＝CD，连接AF．
1. （1）判断直线AF与⊙O的位置关系，并说明理由．
2. （2）若AC＝10，tan∠CAE＝ $\text{[math]}$ ，求AE的长．
答案解析收藏纠错 + 选题
23. (2020九上·庆云期末) “新冠”疫情蔓延全球，口罩成了人们的生活必需品，某药店销售普通口罩和N95口罩，今年8月份的进价如表：

普通口罩

N95口罩

进价（元/包）

8

20
1. （1）计划N95口罩每包售价比普通口罩贵16元，7包普通口罩和3包N95口罩总售价相同，求普通口罩和N95口罩每包售价．
2. （2）按（1）中售价销售一段时间后，发现普通口罩的日均销售量为120包，当每包售价降价1元时，日均销售量增加20包，该药店秉承让利于民的原则，对普通口罩进行降价销售，但要保证当天的利润为320元，求此时普通口罩每包售价．
3. （3）疫情期间，该药店进货3000包N95口罩，进价不变，店长向当地医院捐赠了500包后，又打9折销售，全部售完，这批3000包的N95口罩所获利润为多少元？
答案解析收藏纠错 + 选题
24. (2020九上·庆云期末) 小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．
1. （1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB， AC上，若BC=6，AD=4，求正方形PQMN的边长．
2. （2）操作：能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P′，画正方形P′Q′M′N′，使Q′，M′在BC边上，N′在△ABC内，连结B N′并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．小波把线段BN称为“波利亚线”．
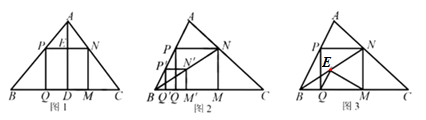
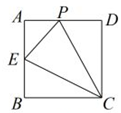
  推理：证明图2中的四边形PQMN是正方形．
3. （3）拓展：在(2)的条件下，于波利业线B N上截取NE=NM，连结EQ，EM(如图3)．当tan∠NBM= $\text{[math]}$ 时，猜想∠QEM的度数，并尝试证明．
  请帮助小波解决“温故”、“推理”、“拓展”中的问题．
答案解析收藏纠错 + 选题
25. (2020九上·庆云期末) 如图，抛物线y=﹣x²+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD.
1. （1）求经过A，B，C三点的抛物线的函数表达式；
2. （2）点Q在该抛物线的对称轴上，若△BCQ是以BC为直角边的直角三角形，求点Q的坐标；
3. （3）若P为BD的中点，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标.
答案解析收藏纠错 + 选题