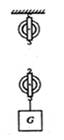B .
B .  C .
C .  D .
D . 



 B .
B . 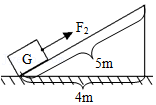 C .
C . 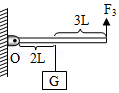 D .
D . 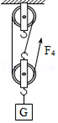

 B . 开瓶器
B . 开瓶器  C . 钓鱼竿
C . 钓鱼竿  D . 大铡刀
D . 大铡刀 

 D . 镊子
D . 镊子 







![]()


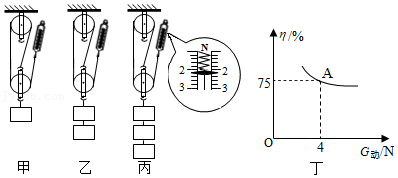
实验1:在直杠杆水平平衡时(如图甲所示)进行实验,记录多组数据。得出:F1×s1=F2×s2(注:s1和s2分别表示支点到F1和F2的作用点的距离)。在直杠杆倾斜平衡时(如图乙所示)进行实验,也得到了同样的结论。

该结论适用于所有平衡时的杠杆吗?
实验2:科学研究小组用一侧弯曲的杠杆进行如图丙所示的实验,移动钩码,改变钩码数量,记录数据如表,分析表格数据发现上述结论并不成立,但发现一个新的等量关系,即:(待填)。
|
实验次数 |
F1/N |
s1/cm |
F2/N |
s2/cm |
l2/cm |
|
1 |
1.0 |
10.0 |
0.5 |
21.3 |
20.1 |
|
2 |
1.5 |
20.0 |
1.0 |
31.7 |
29.8 |
|
3 |
2.0 |
30.0 |
2.5 |
25.5 |
24.0 |
s和l(支点到力的作用线的距离)这两个量在研究杠杆平衡条件时,哪个量才是有价值的呢?研究小组的同学观察到:支点到F的作用点的距离(s1)与支点到F1的作用线的距离(l1)是相等的。研究小组的同学又进行了实验。
实验3:①移动钩码,使杠杆 (待填) 。
②继续实验,使杠杆平衡,记录F1、s1、l1和F2、s2、l2。
③改变钩码数量,移动钩码,记录杠杆处于平衡时的多组F1、s1、l1和F2、s2、l2。
④分析实验数据,得出弯杠杆的平衡条件。
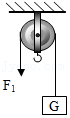
最后,通过科学思维,得出所有杠杆的平衡条件都是:F1×l1=F2×l2。杠杆的平衡条件可用于解释许多杠杆应用,如用图1方式提升物体比用图2方式省力,就可用杠杆的平衡条件作出合理解释。请回答:

|
次数 |
钩码重/N |
钩码上升距离/cm |
弹簧测力计示数/N |
弹簧测力计上升距离/cm |
机械效率/% |
|
1 |
2 |
10 |
0.8 |
30 |
83.3 |
|
2 |
4 |
10 |
1.5 |
30 |
|
|
3 |
6 |
10 |
30 |
90.9 |
|
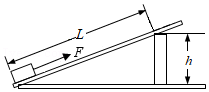
实验序号 |
斜面的倾斜程度 |
物块重力G(牛) |
斜面高度h(米) |
拉力F(牛) |
斜面长度s(米) |
机械效率η |
|
1 |
较缓 |
5 |
0.2 |
2.4 |
1 |
41.7% |
|
2 |
较陡 |
5 |
0.5 |
3.2 |
1 |
78.1% |
|
3 |
最陡 |
5 |
0.7 |
4.3 |
1 |
81.4% |

步骤1;用弹簧测力计在竖直方向用力,使杠杆在水平位置平衡(如图甲),记录弹簧测力计的示数为F1。
步骤2:保持拉力作用点不变,改变拉力的方向,仍让杠杆在水平位置平衡(如图乙),记录弹簧测力计的示数为F2。
步骤3:保持拉力的方向不变,将杠杆下端的硬棒向上移动至A、B、C处,仍让杠杆在水平位置平衡(如图丙),记录弹簧测力计的示分别为FA、FB、FC
请回答下列问题:

|
实验 次数 |
动滑轮重G动/N |
钩码重 G物/N |
钩码上升 高度h物/m |
动力F动/N |
动力作用点移动距离S动/m |
滑轮组的机械效率η |
|
1 |
0.53 |
1 |
0.1 |
0.7 |
0.3 |
47.6% |
|
2 |
2 |
0.1 |
1.1 |
0.3 |
60.6% |
|
|
3 |
4 |
0.1 |
2 |
0.3 |