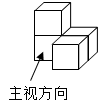
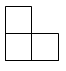
 B .
B . 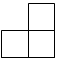 C .
C . 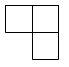 D .
D . 
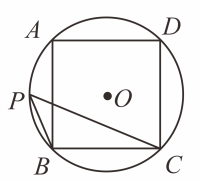


①对于任意实数m,m(m-2b)≥1-2b始终成立,则b=1;②这个函数的顶点始终在抛物线 上;③在-1≤x≤5范围内,y的值最大时,x=-1,点(m1 , p)与点(m2 , p)(m1≠m2)在这个函数图象上,则m1+m2>4;④点(b-2n,y1)与点(b+n,y2)(n≠0)在这个函数图象上,则y1<y2其中错误的结论个数是( )





①求∠AOC度数.
②求点A,C之间的距离.
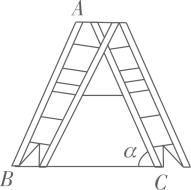
①求证:∆BDC是“近直角三角形”;
②在边AC上是否存在点E(异于点D),使得∆BCE也是“近直角三角形”?若存在,请求出CE的长;若不存在,请说明理由.

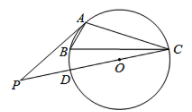
如图1,在∆OAB和∆OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.
填空:①AC与BD之间的数量关系为;②∠AMB的度数为。
如图2,在∆OAB和∆OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请计算AC:BD的值及∠AMB的度数,并说明理由;
在(2)的条件下,将ΔOCD绕点O在平面内旋转,AC,BD所在直线交于点M,若0D=1,OB= ,请求出当点C与点M重合时AC的长.