新疆昌吉州2024年初中学业水平考试数学模拟卷

更新时间：2024-07-19 浏览次数：7 类型：中考模拟

一、单选题(本大题共9小题，每小题4分，共36分)

1. (2024·昌吉模拟) ﹣2024的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . -2024 D . 2024

答案解析收藏纠错 + 选题
2. (2024·昌吉模拟) 某个几何体的展开图如图所示，该几何体是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2024·昌吉模拟) 如图， $\text{[math]}$ 若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024·昌吉模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八上·武汉月考) 点 $\text{[math]}$ 关于 $\text{[math]}$ 轴的对称点 $\text{[math]}$ 的坐标是（）

A . $\text{[math]}$ B . （ $\text{[math]}$ ） C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024·昌吉模拟) 《孙子算经》是中国古代重要的数学著作，是《算经十书》之一．书中记载了这样一个题目：今有木，不知长短．引绳度之，余绳四尺五
寸；屈绳量之，不足一尺．木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余 $\text{[math]}$ 尺；将绳子对折再量长木，长木还剩余 $\text{[math]}$ 尺．问木长多少尺？设木长 $\text{[math]}$ 尺，则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·昌吉模拟) 如图，一次函数 $\text{[math]}$ 的图像与反比例函数 $\text{[math]}$ 的图像相交于A、B两点，点A的横坐标为1，点B的横坐标为 $\text{[math]}$ ，
当 $\text{[math]}$ 时，x的取值范围是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024·昌吉模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 后，得到 $\text{[math]}$ ，点 $\text{[math]}$ 经过的路径为弧 $\text{[math]}$ ，已知 $\text{[math]}$ ，则图中阴影部分的面积为（）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024·昌吉模拟) 如图，已知开口向下的抛物线 $\text{[math]}$ 与x轴交于点 $\text{[math]}$ 对称轴为直线 $\text{[math]}$ ．则下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③函数 $\text{[math]}$
$\text{[math]}$ 的最大值为 $\text{[math]}$ ；④若关于x的方程 $\text{[math]}$ 无实数根，则 $\text{[math]}$ ．正确的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题(本大题共6小题，每小题4分，共24分)

10. (2024·昌吉模拟) 分解因式：2m²-18＝

答案解析收藏纠错 + 选题
11. (2024·昌吉模拟) 若 $\text{[math]}$ 为整数， $\text{[math]}$ 为正整数，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
12. (2024·昌吉模拟) 对某种植物种子进行发芽试验，统计发芽种子数，获得下表：
试验种子数
100
200
400
1000
3000
6000
发芽频数
92
185
374
931
2787
5580
发芽频率
0.92
0.925
0.935
0.931
0.929
0.93
估计该植物种子的发芽概率是.（精确到0.01）

答案解析收藏纠错 + 选题
13. (2024·昌吉模拟) 一个多边形的内角和与外角和之和为900°，则这个多边形的边数为.

答案解析收藏纠错 + 选题
14. (2024·昌吉模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点， $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 边的中点，连接 $\text{[math]}$ ，点 $\text{[math]}$ 为线段 $\text{[math]}$ 上的动点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
15. (2024·昌吉模拟) 如图，正方形ABCD的边长为2，AC ， BD交于点O ，点E为△OAB内的一点，连接AE ， BE ， CE ， OE ，若∠BEC＝90°，给出下列四个结论：① $\text{[math]}$ ；②线段AE的最小值是 $\text{[math]}$ ；③ $\text{[math]}$ ；④ $\text{[math]}$ ．其中正确的结论有 .（填写所有正确结论的序号）

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共90分.解答应写出必要的文字说明、证明过程或演算步骤）

16. (2024·昌吉模拟) 计算：
1. （1） $\text{[math]}$ ．
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2024·昌吉模拟)
1. （1）先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．
2. （2）某停车场的收费标准如下：中型汽车的停车费为15元/辆，小型汽车的停车费为8元/辆．现在停车场内停有30辆中、小型汽车，这些车共缴纳停车费324元，求中、小型汽车各有多少辆？
答案解析收藏纠错 + 选题
18. (2024·昌吉模拟) 如图，在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）判定四边形 $\text{[math]}$ 的形状并说明理由．
答案解析收藏纠错 + 选题
19. (2024·昌吉模拟) 某中学积极落实国家“双减”教育政策，决定增设“礼仪”“陶艺”“园艺”“厨艺”及“编程”等五门校本课程以提升课后服务质量，促进学生全面健康发展为优化师资配备，学校面向七年级参与课后服务的部分学生开展了“你选修哪门课程（要求必须选修一门且只能选修一门）？”的随机问卷调查，并根据调查数据绘制了如下两幅不完整的统计图：
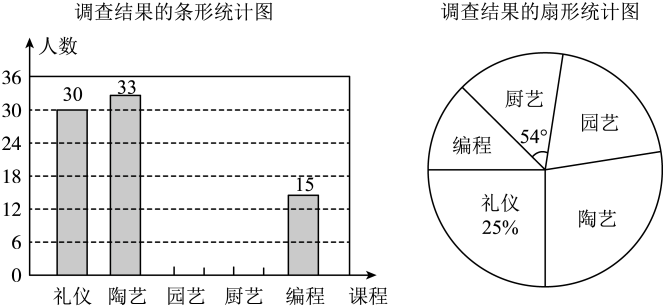
请结合上述信息，解答下列问题：
1. （1）共有名学生参与了本次问卷调查；“陶艺”在扇形统计图中所对应的圆心角是度；
2. （2）补全调查结果条形统计图；
3. （3）小刚和小强分别从“礼仪”等五门校本课程中任选一门，请用列表法或画树状图法求出两人恰好选到同一门课程的概率．
答案解析收藏纠错 + 选题
20. (2024九上·肇源月考) 如图，某座山 $\text{[math]}$ 的项部有一座通讯塔 $\text{[math]}$ ，且点A，B，C在同一条直线上，从地面P处测得塔顶C的仰角为 $\text{[math]}$ ，测得塔底B的仰角为 $\text{[math]}$ ．已知通讯塔 $\text{[math]}$ 的高度为 $\text{[math]}$ ，求这座山 $\text{[math]}$ 的高度（结果取整数）．参考数据： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024·昌吉模拟) 去年防洪期间，某部门从超市购买了一批数量相等的雨衣（单位：件）和雨鞋（单位：双），其中购买雨衣用了400元，购买雨鞋用了350元，已知每件雨衣比每双雨鞋贵5元．
1. （1）求每件雨衣和每双雨鞋各多少元？
2. （2）为支持今年防洪工作，该超市今年的雨衣和雨鞋单价在去年的基础上均下降了20%，并按套（即一件雨衣和一双雨鞋为一套）优惠销售．优惠方案为：若一次购买不超过5套，则每套打九折：若一次购买超过5套，则前5套打九折，超过部分每套打八折．设今年该部门购买了a套，购买费用为W元，请写出W关于a的函数关系式．
3. （3）在（2）的情况下，今年该部门购买费用不超过320元时最多可购买多少套？
答案解析收藏纠错 + 选题
22. (2024·昌吉模拟) 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 是 $\text{[math]}$ 延长线上一点，连接 $\text{[math]}$ ，且 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）若直径 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2024·昌吉模拟) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 分别与x ， y轴交于点A ， B ，抛物线 $\text{[math]}$ 恰好经过这两点．
1. （1）求此抛物线的解析式；
2. （2）若点C的坐标是 $\text{[math]}$ ，将 $\text{[math]}$ 绕着点C逆时针旋转90°得到 $\text{[math]}$ ，点A的对应点是点E ．求：点E的坐标，并判断点E是否在此抛物线上；
3. （3）在(2)的条件下，若点P是y轴上的任一点，求 $\text{[math]}$ 取最小值时，点P的坐标．
答案解析收藏纠错 + 选题