浙江省湖州市长兴县部分学校2021-2022学年九年级下学期...

更新时间：2022-04-11 浏览次数：147 类型：月考试卷

一、选择题（本题有 10小题，每小题 3分，共 30分）

1. (2022九下·长兴月考) 下列二次函数的图象经过原点的是（）

A . y=x²+1 B . y=x²+x C . y=（x+1）² D . y=x²-2x+1

答案解析收藏纠错 + 选题
2. 如图，由图形M改变为图形N，这种图形改变属于（）

A . 平移 B . 轴对称 C . 旋转 D . 相似

答案解析收藏纠错 + 选题
3. (2022九下·长兴月考) 已知α是锐角，若sinα= $\text{[math]}$ ，则α的度数是（）

A . 30° B . 45° C . 60° D . 75°

答案解析收藏纠错 + 选题
4. (2022九下·长兴月考) 比例尺为1：2000的地图上，A，B两地间的图上距离为2cm，则两地间的实际距离是（）

A . 10m B . 20m C . 40m D . 80000m

答案解析收藏纠错 + 选题
5. (2022九下·长兴月考) 如图是某几何体的三视图，这个几何体可以是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2022九下·长兴月考) 如图，PA，PB是⊙O的切线，A，B是切点．若∠P=80° ，则∠ABO的度数是（）

A . 40° B . 45° C . 50° D . 55°

答案解析收藏纠错 + 选题
7. (2022九下·长兴月考) 一个不透明的盒子中装有2个黑球和4个白球，这些球除颜色外其他均相同，从中任意摸出3个球，下列事件为必然事件的是（）

A . 至少有1个黑球 B . 至少有2个黑球 C . 至少有1个白球 D . 至少有2个白球

答案解析收藏纠错 + 选题
8. (2022九下·长兴月考) 如图，若△ABC底边BC上的高为h₁ ， △DEF底边EF上的高为h₂ ，则h₁与h₂的大小关系是（）

A . h₁=h₂ B . h₁<h₂ C . h₁>h₂ D . 以上都有可能

答案解析收藏纠错 + 选题
9. (2022九下·长兴月考) 对于函数y= =ax²-（a+1）x+1，甲和乙分别得出一个结论：
甲：若该函数图象与x轴只有一个交点，则a=1；

乙：方程ax²- （a+1）x+1=0至少有一个整数根．

甲和乙所得结论的正确性应是（）

A . 只有甲正确 B . 只有乙正确 C . 甲乙都正确 D . 甲乙都不正确

答案解析收藏纠错 + 选题
10. (2022九下·长兴月考) 如图，AB是⊙O的直径，CD⊥AB于点E，连结CO并延长，交弦AD于点F．若AB=10，BE=2，则OF的长度是（）

A . $\text{[math]}$ B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本题有6小题，每小题4分，共24分）

11. (2022九下·长兴月考) 若2a=3b，则a:b=.

答案解析收藏纠错 + 选题
12. (2022九下·长兴月考) 投掷一枚质地均匀的正方体骰子，朝上一面的点数恰好是1的概率是．

答案解析收藏纠错 + 选题
13. (2022九下·长兴月考) 如图，点A，B，C，D，E在⊙O上，且 $\text{[math]}$ 的度数为50°，∠ACD= 60°，则∠E的度数是

答案解析收藏纠错 + 选题
14. (2022九下·长兴月考) 如图，已知线段AB=6，分别以端点A，B为圆心，大于 $\text{[math]}$ AB的长为半径作弧，两弧交于点M，N，点C，D在直线MN上，连结AC，CB，BD，DA．若点E，F分别是AC和AD的中点，且CD=8，则△BEF的面积是

答案解析收藏纠错 + 选题
15. (2022九下·长兴月考) 如图，已知在Rt△AOB中，∠AOB=90°，⊙O与AB相交于点C，与BO相交于点D，连结CD，CO．若∠BOC=2∠BCD，AO=15，AB=25，则BD的长是

答案解析收藏纠错 + 选题
16. (2022九下·长兴月考) 如图是王明正在设计的一动画示意图，×轴上依次有A，B，C三个点，且AB=2，在BC上方有五个台阶（各拐角均为90°），每个台阶的高、宽分别是1和1.5，第一个台阶到x轴距离BD=10．从点A处向右，上方沿抛物线y=-x²+4x+12发出一个带光的点P．当点P落在台阶上时，落点的坐标是．

答案解析收藏纠错 + 选题

三、解答题（本题有8小题，共66分）

17. (2022九下·长兴月考) 如图，已知扇形AOB的圆心角为120°，半径OA为6cm．求扇形AOB的弧长和面积．

答案解析收藏纠错 + 选题
18. (2022九下·长兴月考) 如图，直线l₁∥l₂∥l₃ ，直线AC依次交l₁ ， l₂ ， l₃于A，B，C三点，直线DF依次交l₁ ， l₂ ， l₃于D，E，F三点，若 $\text{[math]}$ ，DE=12，求EF的长．

答案解析收藏纠错 + 选题
19. (2022九下·长兴月考) 如图，升国旗时，某同学站在离国旗20m的E处行注目礼（即BE=20m），当国旗升至旗杆顶端A时，该同学视线的仰角∠ADC=42°，已知他的双眼离地面的高度DE=1.60m．求旗杆AB的高度（结果精确到0.01m）．
参考数据：sin42°≈0.6691，cos42°≈0.7431，tan42°≈0.9004．

答案解析收藏纠错 + 选题

20. (2022九下·长兴月考) 某校在疫情期间开展线上教学，学生从“录播”和“直播”两种教学方式中选择一种．为分析该校学生线上学习情况，在接受这两种教学方式的学生中各随机抽取40人调查学习参与度，数据整理结果如下表（数据分组包含左端值不包含右端值）：

人数

参与度

方式

0.2~0.4

0.4~0.6

0.6~0.8

0.8~1

录播

直播

（1）从选择教学方式为“录播”的学生中任意抽取一位学生，估计该学生的参与度在0.8及以上的概率是多少；
（2）若该校共有600名学生选择“直播”，估计其中参与度在0.4以下的共有多少人

答案解析收藏纠错 + 选题

21. (2022九下·长兴月考) 如图，已知等边△ABC的边长为6，点O是AB边上的一点，以OA为半径的⊙O与边AC，AB分别交于点D，E，过点D作DF⊥BC于点F．
1. （1）求证：DF是⊙O的切线；
2. （2）连结EF，当EF是⊙O的切线时，求⊙O的半径．
答案解析收藏纠错 + 选题
22. (2022九下·长兴月考) 某商贸公司购进某种商品的成本为20元/千克，经过市场调研发现，这种商品在未来40天的销售单价y（元/千克）与时间×（天）之间的函数关系式为：y= $\text{[math]}$ ，且×为整数，且日销量m（千克）与时间×（天）之间的变化规律符合一次函数关系，如下表：

时间x（天）

1

3

6

10

……

日销量m（千克）

142

138

132

124

……
1. （1）求m与×的函数关系式；
2. （2）当1≤×≤20时，最大日销售利润是多少？
3. （3）求：在未来40天中，有多少天销售利润不低于1550元？
答案解析收藏纠错 + 选题
23. (2022九下·长兴月考) 已知△ABC和△DEC都为等腰三角形，AB=AC，DE=DC，∠BAC=∠EDC=n°．
1. （1）当n=60时，如图1，当点D不在AC上时，判断线段BE与AD的数量关系，并说明理由；
2. （2）当n=90时，
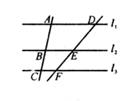
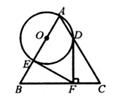
  ①如图2，探究线段BE与AD的数量关系，并说明理由；
  
  ②当BE∥AC，AB=3 $\text{[math]}$ ，AD=1时，求CE的长．
答案解析收藏纠错 + 选题
24. (2022九下·长兴月考) 已知抛物线y=ax²+bx+c（a≠0）的顶点在×轴上．
1. （1）若抛物线过点P（0， $\text{[math]}$ ），求证：a=b²？；
2. （2）已知点P₁（-2，1），P₂（2，-1），P₃（2，1）中恰有两点在抛物线上
  ①求抛物线的解析式；
  
  ②设直线l：y= $\text{[math]}$ x+1与抛物线交于A，B两点，点M在直线y=n（n<0）上，过A，B两点分别作直线y=n（n<0）的垂线，垂足为C，D．是否存在这样的n的值，使得以点A，C，M为顶点的三角形与△BDM相似的点M恰有两个？若存在，请直接写出n的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题