浙江省宁波市2022年中考数学模拟预测数学试卷

更新时间：2022-04-30 浏览次数：268 类型：中考模拟

一、单选题

1. (2022·宁波模拟) 计算：|1﹣2022|＝（）

A . 2021 B . ﹣2021 C . 2022 D . ﹣2020

答案解析收藏纠错 + 选题
2. (2022·宁波模拟) 计算2cos30°的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022·宁波模拟) 下列图形中，既是中心对称图形，又是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·宁波模拟) 习近平总书记在决战决胜脱贫攻坚座谈会上的讲话中指出，2021年脱贫攻坚任务完成后，我国有110000000左右贫困人口实现脱贫，将“110000000”用科学记数法可表示为（）

A . 1.1×10⁷ B . 1.1×10⁸ C . 1.1×10⁹ D . 1.1×10¹⁰

答案解析收藏纠错 + 选题
5. (2022·宁波模拟) 如图，△ABC中，∠A=30°，点O是边AB上一点，以点O为圆心，以OB为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD=2 $\text{[math]}$ ，则线段CD的长是（）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·柯桥模拟) 如图是某商场一楼与二楼之间的手扶电梯示意图.其中 $\text{[math]}$ 、 $\text{[math]}$ 分别表示一楼、二楼地面的水平线， $\text{[math]}$ ， $\text{[math]}$ 的长是 $\text{[math]}$ ，则乘电梯从点 $\text{[math]}$ 到点 $\text{[math]}$ 上升的高度 $\text{[math]}$ 是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·宁波模拟) 篮球小组共有15名同学，在一次投篮比赛中，他们的成绩如右面的条形图所示，这15名同学进球数的众数和中位数分别是（）

A . 6，7 B . 7，9 C . 9，7 D . 9，9

答案解析收藏纠错 + 选题
8. (2022·宁波模拟) 在四边形ABCD中，将下列条件中的任意两个进行组合，可以判定它是平行四边形的有（）组.
（1）AB∥CD （2）AD∥BC（3）AB=CD（4）AD=BC（5）∠A=∠C（6）∠B=∠D

A . 7 B . 8 C . 9 D . 10

答案解析收藏纠错 + 选题
9. (2022·宁波模拟) 如图，二次函数y=ax²+bx+c的部分图象如图，在下面五个结论中：①ac＜0；②a+b+c＞0；③2a﹣b＞0；④只有当 $\text{[math]}$ 时，完整的函数图象与坐标轴有两个交点；⑤如果在直线 $\text{[math]}$ 的右侧函数值随着x的增大而增大，那么a=2.其中正确的结论有（）个

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
10. (2022·宁波模拟) $\text{[math]}$ ABCD被分别平行于两边的四条线段EJ、FI、LG、KH分割成9个小平行四边形，面积分别为S_1-9 ，已知 $\text{[math]}$ ALME∽ $\text{[math]}$ PICH∽ $\text{[math]}$ ABCD.若知道S_1-9中的n个，就一定能算出平行四边形ABCD的面积，则n的最小值是（）.

A . 2 B . 3 C . 4 D . 6

答案解析收藏纠错 + 选题

二、填空题

11. (2022·宁波模拟) 计算a⁶÷a²的结果等于．

答案解析收藏纠错 + 选题
12. (2022·宁波模拟) 正十边形的每个外角都等于度．

答案解析收藏纠错 + 选题
13. (2022·宁波模拟) 不等式组 $\text{[math]}$ 的整数解的和为.

答案解析收藏纠错 + 选题
14. (2024九下·秦淮模拟) 为了了解某区初中学生的视力情况，随机抽取了该区500名初中学生进行调查.整理样本数据，得到下表：

视力

4.7以下

4.7

4.8

4.9

4.9以上

人数

102

98

80

93

127

根据抽样调查结果，估计该区12000名初中学生视力不低于4.8的人数是.

答案解析收藏纠错 + 选题
15. (2022·宁波模拟) 如图，直线L：y=-x+1与坐标轴交于A、B两点，点C是反比例函数 $\text{[math]}$ （x＞0）图象上任意一点，过C分别作横纵轴的垂线CD、CG，交线段AB于E、F两点.设OE=a，EF=b，FA=c，请写出在点C移动过程中，a、b、c保持不变的数量关系.

答案解析收藏纠错 + 选题
16. (2022·宁波模拟) 太极推盘是一种常见的健身器材（如图1），转动两个圆盘便能锻炼身体.取推盘上半径均为0.4米的圆A与圆B（如图2）且AB=1米，圆A绕圆心A以2°每秒的速度逆时针旋转，圆B绕圆心B以2°每秒的速度顺时针旋转.开始转动时圆A上的点C恰好落在线段AB上，圆B上的点D在AB下方且满足∠DBA=60°，则在两圆同时开始转动的30秒内，CD的最小值是米.

答案解析收藏纠错 + 选题

三、解答题

17. (2022·宁波模拟) 先化简，再求值：（x + 1）x -（x + 3）（x - 3），其中x = 2.

答案解析收藏纠错 + 选题
18. (2022·宁波模拟) 中考体育测试前，某区教育局为了了解选报引体向上的九年级男生的成绩情况，随机抽查了本区部分选报引体向上项目的九年级男生的成绩，并将测试得到的成绩绘成了下面两幅不完整的统计图.请你根据图中的信息，解答下列问题：
1. （1）写出扇形图中a=_%，本次抽测中，成绩为6个的学生有_名.
2. （2）求这次抽测中，测试成绩的众数和中位数；
3. （3）该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考选报引体向上的男生能获得满分的有多少名？
答案解析收藏纠错 + 选题
19. (2022·宁波模拟) 请尺规作图完成下列画图，不写画法，保留画图痕迹.
1. （1）如图 1，E在矩形纸片ABCD的边AD上，将纸片折叠，使AB落在CE所在直线上，画出折痕MN（点M，N分别在边AD，BC上）；
2. （2）如图 2，点 A、B、C 均在⊙O 上，且∠BAC=120°，在优弧 BC上画 M、N 两点，使∠MAN=60°.
答案解析收藏纠错 + 选题
20. (2022·宁波模拟) 小美周末来到公园，发现在公园一角有一种“守株待兔”游戏.游戏设计者提供了一只兔子和一个有 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的.规定：①玩家只能将小兔从A，B两个出入口放入；②如果小兔进人笼子后选择从开始进入的出入口离开，则可获得一只价值4元的小兔玩具，否则应付费3元.
1. （1）请用画树状图的方法，列举出该游戏的所有可能情况；
2. （2）小美得到小兔玩具的机会有多大?
3. （3）假设有125人次玩此游戏，估计游戏设计者可赚多少元.
答案解析收藏纠错 + 选题
21. (2022·兰溪模拟) 如图①，将南北向的中山路与东西向的北京路看成两条直线，十字路口记作点A.甲从中山路上点B出发，a米/分的速度骑车向北匀速直行；与此同时，乙从点A出发沿北京路以b米/分的速度步行向东匀速直行.设出发x分钟时，甲、乙两人与点A的距离分别为y₁、y₂米.已知y₁、y₂ ，则y₁、y₂与x之间的函数关系如图②所示.
1. （1）分别写出y₁、y₂关于x的函数表达式（用含有a、b的式子表示）；
2. （2）求a、b的值.
答案解析收藏纠错 + 选题
22. (2022·宁波模拟) 疫情形势依然严峻，我们需要继续坚持常态化防控.卫生专家建议多补充维生素增强身体免疫力以抵御病菌，现有甲、乙、丙3种食物的维生素含量和成本如下表：

甲种食物
乙种食物
丙种食物
维生素A(单位/kg)
300
600
300
维生素B(单位/kg)
700
100
300
成本(元/kg)
6
4
3
某食品公司欲用这3种食物研制100千克食品，要求研制成的食品中至少含有36000单位的维生素A和40000单位的维生素B.
1. （1）研制100千克食品，甲种食物至少要用多少千克？丙种食物至多能用多少千克？
2. （2）若限定甲种食物用50千克，则研制这100千克食品的总成本S的取值范围是多少？
答案解析收藏纠错 + 选题
23. (2022·宁波模拟) 定义：在一个等腰三角形底边的高线上所有点中，到三角形三个顶点距离之和最小的点叫做这个等腰三角形的“近点”，“近点”到三个顶点距离之和叫做这个等腰三角形的“最近值”.
1. （1）【基础巩固】
  如图1，在等腰Rt△ABC中，∠BAC=90°，AD为BC边上的高，已知AD上一点E满足∠DEC=60°，AC= $\text{[math]}$ ，求AE+BE+CE=.
2. （2）【尝试应用】
  如图2，等边三角形ABC边长为 $\text{[math]}$ ， E为高线AD上的点，将三角形AEC绕点A逆时针旋转60°得到三角形AFG，连接EF，请你在此基础上继续探究等边三角形ABC的“近点”P与D的距离，并求出等边三角形ABC的“最近值”.
3. （3）【拓展提高】
  如图3，在菱形ABCD中，过AB的中点E作AB垂线交CD的延长线于点F，连接AC、DB，已知∠BDA=75°，AB=6，求三角形AFB“最近值”的平方.
答案解析收藏纠错 + 选题
24. (2022·宁波模拟) CD是以O为圆心AB为直径的半圆上的弦，E、F是弦CD上的点，线段BF与线段EO交于点G、与线段DO交于点H.
1. （1）如图1，当点E为CD中点，点F与点C重合时，若tan∠DOB= $\text{[math]}$ ， CD=12，求EG；
2. （2）如图2，当弦CD∥AB，AO=10，BH=7，HG= $\text{[math]}$ ，求OH：OG；
3. （3）在（2）的条件下，若CD=16.
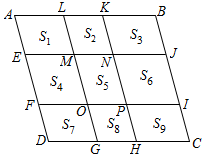
  ①求OE；
  ②求S_△_GHO—S_△_EFG.
答案解析收藏纠错 + 选题