山东省青岛市市南区2022年中考数学一模试题

更新时间：2024-07-13 浏览次数：99 类型：中考模拟

一、单选题

1. (2022·绿园模拟) $\text{[math]}$ 的倒数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·市南区模拟) 下列四个图案中是轴对称图形的个数是（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
3. (2022·市南区模拟) 由一些相同的小立方块组成的几何体的三种视图如图所示，则组成这个几何体的小立方块的个数是（）

A . 4个 B . 5个 C . 6个 D . 7个

答案解析收藏纠错 + 选题
4. (2022·市南区模拟) 为了保护环境加强环保教育，某中学组织学生参加义务收集废旧电池的活动，下面是随机抽取的42名学生收集废旧电池数量的统计表：
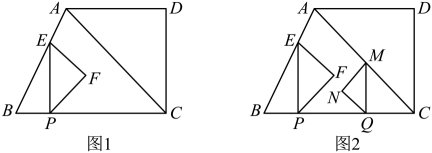
废旧电池数/节
4
5
6
7
人数/人
9
12
12
9
请根据学生收集到的废旧电池数，判断下列说法正确的是（）

A . 样本为42名学生 B . 众数是9节和12节 C . 中位数是6节 D . 平均数是5.5节

答案解析收藏纠错 + 选题
5. (2022·市南区模拟) 北京冬奥会于2022年2月4日在中华人民共和国国家体育场举行．在此期间，国家体育总局委托国家统计局开展的“带动三亿人参与冰雪运动”统计调查数据显示，全国居民参与过冰雪运动的人数为346000000人，将346000000用科学记数法表示为（）

A . 3.46×10⁷ B . 3.46×10⁸ C . 34.6×10⁸ D . 3.46×10¹⁰

答案解析收藏纠错 + 选题
6. (2022·市南区模拟) 如图，以某网格线所在直线建立平面直角坐标系，将△ABC绕点P旋转180°得到△DEF，已知点A（2，-1），点P的坐标为（）

A . （-2，2） B . （2，-2） C . （1，-3） D . （-3，1）

答案解析收藏纠错 + 选题
7. (2022·市南区模拟) 如图，AB是☉O的直径，点C、D是圆上的两点，若∠AOC=116°，则∠CDB的度数为（）

A . 32° B . 22° C . 37° D . 27°

答案解析收藏纠错 + 选题
8. (2022·市南区模拟) 已知点M（-1，1）与反比例函数 $\text{[math]}$ 的图象如图所示，则二次函数 $\text{[math]}$ 的图象大致为（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2022八下·高唐期末) 计算 $\text{[math]}$ ÷3 $\text{[math]}$ × $\text{[math]}$ 的结果是．

答案解析收藏纠错 + 选题
10. (2022·市南区模拟) 林业部门要观察某种树苗在一定条件下的移植成活率，下表是这种树苗在移植过程中的一组数据：
移植的棵数n
1000
1500
2500
4000
8000
15000
20000
30000
成活的棵数m
853
1356
2220
3500
7056
13170
17580
26400
成活的频率 $\text{[math]}$
0.853
0.904
0.888
0.875
0.882
0.878
0.879
0.880
根据以上数据，该林业部门估计在此条件下移植的55000棵树苗成活的棵数约为．

答案解析收藏纠错 + 选题
11. (2022·市南区模拟) 如图，在☉O中，弦CD与直径AB平行，CD=OA=2，则阴影部分的面积为．

答案解析收藏纠错 + 选题
12. (2024九下·青岛模拟) 某海洋养殖场每年的养殖成本包括固定成本和可变成本，其中固定成本每年均为4万元，可变成本逐年增长，已知该养殖场第一年的可变成本为2.6万元，第三年的养殖成本为7.146万元，设可变成本平均每年增长的百分率为x，则可列方程为．

答案解析收藏纠错 + 选题
13. (2022·市南区模拟) 如图，在正方形ABCD的边长为6，对角线AC、BD相交于点O，点E、F分别在BC、CD的延长线上，且CE=3，DF=2，G为EF的中点，连接OE，交CD于点H，连接GH，则GH的长为．

答案解析收藏纠错 + 选题
14. (2022·市南区模拟) 二次函数 $\text{[math]}$ (a、b、c实常数，且a≠0)的函数值y与自变量x的部分对应值如下表：
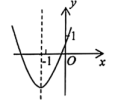
x
…
-1
0
1
2
…
y
…
m
2
2
n
…
且当 $\text{[math]}$ 时，对应的函数值y＜0．有以下结论：①abc＞0；②m+n＜ $\text{[math]}$ ；③关于x的方程 $\text{[math]}$ 的负实数根在 $\text{[math]}$ 和0之间；④P₁(t-1，y₁)和P₂(t+1，y₂)在该二次函数的图象上，则当实数t＞ $\text{[math]}$ 时，y₁＞y₂ ．其中正确的结论是．

答案解析收藏纠错 + 选题

三、解答题

15. (2022·市南区模拟) 如图，已知Rt△ABC，∠C=90°；
求作：一个面积最大的等腰直角△CDE，使等腰直角三角形的斜边CE在边BC上．

答案解析收藏纠错 + 选题
16. (2022·市南区模拟) 计算
1. （1）化简： $\text{[math]}$ ；
2. （2）解不等式组 $\text{[math]}$ ，并求出所有非负整数解．
答案解析收藏纠错 + 选题
17. (2022·市南区模拟) 小颖和小丽做“摸球”游戏：在一个不透明的袋子中装有编号为：1、2、4的三个球（除编号外都相同），从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字．若两次数字之和为奇数，则小颖胜；若两次数字之和为偶数，则小丽胜．试分析这个游戏对双方是否公平？请用树状图或列表法说明理由．

答案解析收藏纠错 + 选题
18. (2022·市南区模拟) 某市在全市中学开展了以“预防新冠，人人有责”为主题的知识竞赛活动．为了解学生在此次竞赛中的成绩情况，某校随机抽取了部分学生的竞赛成绩进行统计（满分：100分，等次：A.优秀：90～100分；B.良好：80～89分；C.一般：60～79分；D.较差：60分以下，成绩均为整数）得到如下不完整的图表：
等次
频数
频率
A
m
0.25
B
n
0.5
C
30
b
D
20
0.1
根据以上信息解答下列问题：
1. （1）该校本次被抽查的学生共有多少人？
2. （2）补全图中条形统计图；
3. （3）若该校共有学生2300人，请根据上述调查结果估计该校学生成绩在良好及以上的学生约有多少人？（写出计算过程）
答案解析收藏纠错 + 选题
19. (2023·青岛模拟) 如图，斜坡AB的坡角为33°，BC⊥AC，现计划在斜坡AB中点D处挖去部分坡体，用于修建一个平行于水平线CA且长为12m的平台DE和一条坡角为45°的新的陡坡BE．建筑物GH距离A处36米远（即AG为36米），小明在D处测得建筑物顶部H的仰角为36°．图中各点均在同一个平面内，且点C、A、G在同一条直线上，HG⊥CG，求建筑物GH的高度．（结果精确到1m）
（参考数据：sin33° $\text{[math]}$ ， cos33° $\text{[math]}$ ， tan33° $\text{[math]}$ ， sin36° $\text{[math]}$ ， cos36° $\text{[math]}$ ， tan36° $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2022·市南区模拟) 某商场计划在年前用40000元购进一批新款衬衫进行销售，由于进货厂商促销，实际以8折的价格购进这次衬衫，结果比原计划多购进80件．
1. （1）该商场实际购进每件衬衫多少元？
2. （2）该商场打算在进阶的基础上，每件衬衫加价50%进行销售．由于接近年底，可能会出现滞销，因此会有20%的衬衫需要打5折降价出售，该商场要想获得不低于20000元的利润，应至少再购进衬衫多少件？
答案解析收藏纠错 + 选题
21. (2022·市南区模拟) 如图，矩形ABCD的对角线AC与BD相较于点O，∠EAC=∠BAC，CE⊥AE，交AD于点F，连接DE、OF．
1. （1）求证：OF⊥AC；
2. （2）当∠BAC与∠ACB满足什么数量关系时，四边形AODE是菱形？请说明理由．
答案解析收藏纠错 + 选题
22. (2022·市南区模拟) 某电子公司前期投入240万元作为某种电子产品的研发费用，成功研制出这种市场热销的电子产品，已于当年投入生产并进行销售．已知生产这种电子产品的成本为8元/件，在销售过程中发现：每年的年销售量y（万件）与销售价格x（元/件）的关系如图所示．设该电子公司销售这种电子产品的年利润为S（万元）．（注：若上一年盈利，则盈利不计入下一年的年利润；若上一年亏损，则亏损计作下一年的成本）
1. （1）请求y（万件）与销售价格x（元/件）之间的出函数关系式；
2. （2）求出第一年这种电子产品的年利润S（万元）与销售价格x（元/件）之间的出函数关系式，并求出第一年年利润的最大值（第一年年利润=总售价-总成本-研发费用）；
3. （3）假设公司的这种电子产品第一年恰好按年利润S（万元）取得最大值时进行销售，现根据第一年的盈亏情况，决定第二年将这种电子产品每件的销售价格x定在12元以上（x＞12），若年销售量与每件销售价格仍满足（1）的关系，当第二年的年利润不低于44万元时，求出第二年销售量的最大值．
答案解析收藏纠错 + 选题
23. (2022·市南区模拟) 定义：有一组邻边相等且对角互补的四边形叫做等补四边形．
1. （1）【问题理解】
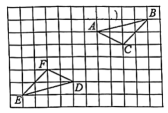
  如图1，在☉O上有三个点A、B、C，连接AB、BC．现要在☉O上再取一点D，使得四边形ABCD是等补四边形，请写出点D的一种取法，并证明你得到的四边形ABCD是等补四边形．
2. （2）【拓展探究】
  如图2，在等补四边形ABCD中，AB=AD
  ①已知BC：CD=7：4，△ACD的面积为8，则四边形ABCD的面积为 ▲ ；
  ②连接AC，请在图中找出一组具有相等关系的角，并证明你的结论．
3. （3）【问题解决】
  如图3，在等补四边形ABCD中，AB=AD，其外角∠EAD的平分线交CD的延长线于点F．若CD=7，DF=3，且AF的长．
答案解析收藏纠错 + 选题
24. (2022·市南区模拟) 已知，如图1，在四边形ABCD中，AD//BC，∠BCD=90°，AD=CD=6，tanB=3，动点P从B出发，以每秒1个单位长度的速度沿BC方向运动，过点P作PE⊥BC，交折线BA-AD于点E，以PE为斜边向右作等腰直角三角形PEF，设点P的运动时间为t秒（t＞0）
1. （1）当t为何值时，点F恰好落在CD上？
2. （2）若P与C重合时运动结束，在整个运动过程中，设等腰直角三角形PEF与四边形ABCD重叠部分的面积为S，请求S关于t之间的函数关系式；
3. （3）当F在CD右侧时，是否存在某一时刻，使得重叠部分的面积S与四边形ABCD重叠部分的面积比为1：8？若存在，求出t的值；若不存在，请说明理由；
4. （4）如图2，在点P开始运动时，BC上另一点Q同时从点C出发，以每秒2个单位长度的速度沿CB方向运动，当Q到达B点时停止运动，同时点P也停止运动，过点Q作QM⊥BC，交射线CA于点M，以QM为斜边向左作等腰直角三角形QMN，若两个等腰直角三角形分别有一条边恰好在一条直线上，请直接写出t的值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

山东省青岛市市南区2022年中考数学一模试题

副标题：

*注意事项：

山东省青岛市市南区2022年中考数学一模试题

试题分析

总体分析

题量分析

难度分析

知识点分析

移植的棵数n	1000	1500	2500	4000	8000	15000	20000	30000
成活的棵数m	853	1356	2220	3500	7056	13170	17580	26400
成活的频率 $\text{[math]}$	0.853	0.904	0.888	0.875	0.882	0.878	0.879	0.880

废旧电池数/节	4	5	6	7
人数/人	9	12	12	9

x	…	-1	0	1	2	…
y	…	m	2	2	n	…

等次	频数	频率
A	m	0.25
B	n	0.5
C	30	b
D	20	0.1