陕西省榆林市榆阳区2022年初中学业水平数学二模试卷

更新时间：2022-07-19 浏览次数：58 类型：中考模拟

一、单选题

1. (2022·榆阳模拟) 妈妈的微信账单明细中 $\text{[math]}$ 元表示收入40元，那么 $\text{[math]}$ 元表示（）

A . 收入25元 B . 支出25元 C . 收入15元 D . 支出15元

答案解析收藏纠错 + 选题
2. (2022·榆阳模拟) 如图，下列四个有机物的结构简式中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·榆阳模拟) 唐长安城遗址是世界史上最大的国际大都会遗址，城址面积达83100000平方米，将83100000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2022七下·萧县期末) 如图， $\text{[math]}$ 于点C，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·榆阳模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点D、E、F分别为边 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点P，则 $\text{[math]}$ 的长为（）

A . 8 B . 7 C . 6 D . 5

答案解析收藏纠错 + 选题
6. (2022·榆阳模拟) 已知直线 $\text{[math]}$ 向下平移2个单位长度后得到直线 $\text{[math]}$ ，且直线 $\text{[math]}$ 与直线 $\text{[math]}$ 关于y轴对称，则k的值为（）.

A . $\text{[math]}$ B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
7. (2022·榆阳模拟) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E、G分别为边 $\text{[math]}$ 、 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相交于点F，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 6 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
8. (2022·榆阳模拟) 二次函数 $\text{[math]}$ 的图象如图所示，已知其对称轴为 $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2022·榆阳模拟) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2022·榆阳模拟) 已知某正多边形一个外角的度数为 $\text{[math]}$ ，则过该正多边形的一个顶点的对角线有条.

答案解析收藏纠错 + 选题
11. (2022·榆阳模拟) 在计算机程序中，二叉树是指每个结点最多有两个子树的树结构，如图，一层二叉树的结点总数为1，二层二叉树的结点总数为3，三层二叉树的结点总数为7……照此规律，五层二叉树的结点总数为.

答案解析收藏纠错 + 选题
12. (2022·榆阳模拟) 已知 $\text{[math]}$ ，点 $\text{[math]}$ 在某反比例函数的图象上，若该反比例函数的图象也经过点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间的大小关系是.（用“＜”连接）

答案解析收藏纠错 + 选题
13. (2022·榆阳模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的对角线，点P为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，若 $\text{[math]}$ 和 $\text{[math]}$ 的面积分别为3和13，则 $\text{[math]}$ 的面积为.

答案解析收藏纠错 + 选题

三、解答题

14. (2022八下·西双版纳期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2022·榆阳模拟) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2022·榆阳模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2023九上·西安期末) 如图，在 $\text{[math]}$ 中，请用尺规作图法，在 $\text{[math]}$ 边上找一点 $\text{[math]}$ ，使 $\text{[math]}$ .（保留作图痕迹，不写作法）

答案解析收藏纠错 + 选题
18. (2022·榆阳模拟) 如图，矩形 $\text{[math]}$ 的对角线 $\text{[math]}$ 、 $\text{[math]}$ 相交于点O，过点B作 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形.

答案解析收藏纠错 + 选题
19. (2022·榆阳模拟) 我国古代数学名著《张邱建算经》中记载：“今有清酒一斗直粟十斗，醑酒一斗直粟三斗，今持粟三斛，得酒五斗，问清、醑酒各几何？”译文：现在一斗清酒价值10斗谷子，一斗醑酒价值3斗谷子，现在拿30斗谷子，共换了5斗酒，问清、醑酒各几斗？

答案解析收藏纠错 + 选题
20. (2022·榆阳模拟) 近日，全国首座考古学科专题博物馆——陕西考古博物馆于西安正式建成，馆内基本陈列以“考古圣地华章陕西”为主题，分为“考古历程”“文化谱系”“考古发现”“文保科技”四大篇章.九年级（1）班班主任组织全班同学参观完该博物馆后，班长将一个可自由转动的转盘平均分成四个相等的扇形，并分别标上A.考古历程、B.文化谱系、C.考古发现、D.文保科技，如图，每个同学转动一次转盘，转盘停止后，就指针所指扇形对应的篇章写一篇观后感（若指针刚好落在分割线上，则需重新转动转盘，直到指针指向某一扇形为止），已知小青和小英都是九年级（1）班的同学.
1. （1） “小背转动一次转盘，转盘停止后指针指向A.考古历程”是事件；（填“必然”或“随机”或“不可能”）
2. （2）请用列表法或画树状图的方法求小青和小英所写观后感的篇章不同的概率.
答案解析收藏纠错 + 选题
21. (2022·榆阳模拟) 榆林市新闻大厦设计融合了陕北窑洞和民间剪纸艺术，“H”型的双塔建筑隐寓榆林开诚、开放、开明、开创的城市精神，大厦双塔建筑既独立又统一的建筑艺术美，是西部地区文化传媒类项目中的精品.某实践小组欲测量新闻大厦的高度，如图为新闻大厦的大致结构示意图（其底部B处可以到达，顶部A处不易到达，且 $\text{[math]}$ 垂直于地面），请你根据下列条件，帮该实践小组设计一种测量方案：
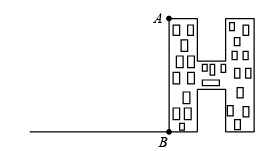
条件一：测量可以在有阳光的晴日里进行；
条件二：测量者只备有①一根标杆、②一面平面镜、③一卷足够长的皮卷尺三种工具.
1. （1）你所选用的测量工具是；（填序号）
2. （2）请在图中画出测量示意图并写出测量数据（不要求写出测量过程）；（线段长度用a，b，c……表示）
3. （3）根据你的测量数据，计算该新闻大厦的高度 $\text{[math]}$ .（用含a、b、c……的式子表示）
答案解析收藏纠错 + 选题
22. (2022·榆阳模拟) 在五四青年节即将到来之际，习近平总书记25日到中国人民大学考察调研，考察期间，总书记尤其注重“红色”这一底色，他强调，“一定要把这一光荣传统和红色基因传承好”，“赓续红色血脉”.为引导广大背少年竖立正确的世界观、人生观、价值观，传承红色基因，某校进行了一次以“弘扬红色文化·传承红色基因”为主题的绘画作品征集活动.张老师从全校随机抽取了4个班（用A，B，C，D表示），对征集到的作品数量进行了统计分析，并将统计结果绘制成如下两幅不完整的统计图，根据统计图中的信息，解答下列问题：
1. （1）补全条形统计图，并计算扇形统计图中A所在扇形的圆心角度数；
2. （2）请计算张老师抽取的4个班平均每班征集到的作品件数；
3. （3）若该校共有30个班级，请你估计学校此次共征集到多少件作品？
答案解析收藏纠错 + 选题
23. (2022·榆阳模拟) 近日，教育部印发了《义务教育课程方案和课程标准（2022年版）》，新课程、课标将于2022年秋季学期开始执行，这其中，“体育与健康”总课时比例超越外语，与此同时，新课标还明确要求教师应在提高课内教学质量的基础上，积极组织、指导学生参与校内多种形式的课外体育活动和竞赛活动.某体育用品商店为抓住商机，准备购进篮球和足球共200个进行销售，已知每个篮球和足球的进价和售价如下表所示：

篮球
足球
进价（元/个）
150
40
售价（元/个）
180
60
设商店购进篮球的数量为x个，售完这200个球所获总利润为y元.（利润＝售价－进价）
1. （1）求y与x之间的函数关系式；
2. （2）结合学生的实际爱好情况，商店决定购进的篮球数量不超过足球数量的3倍，求该商店购进篮球和足球各多少个时，才能使售完这200个球所获总利润最大？最大总利润为多少？
答案解析收藏纠错 + 选题
24. (2022·榆阳模拟) 如图， $\text{[math]}$ 为 $\text{[math]}$ 的内接三角形， $\text{[math]}$ 为 $\text{[math]}$ 的直径，点D为 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，过点D作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点E.
1. （1）求证： $\text{[math]}$ 为 $\text{[math]}$ 的切线；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的半径.
答案解析收藏纠错 + 选题
25. (2022·榆阳模拟) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 与x轴交于点A、B（点A在点B的右侧），与y轴交于点C，且 $\text{[math]}$ ，点F为点C关于x轴的对称点，连接 $\text{[math]}$ .
1. （1）求抛物线的函数表达式；
2. （2）若点E为抛物线的对称轴上一点，在抛物线上是否存在点D，使得以点B、F、D、E为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由.
答案解析收藏纠错 + 选题
26. (2022·榆阳模拟)
1. （1）【问题提出】如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点D，设 $\text{[math]}$ 的长为m，点D到边 $\text{[math]}$ 的距离为n，则mn；（填“＞”“＜”或“＝”）
2. （2）【问题探究】
  如图2，在梯形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为对角线，且 $\text{[math]}$ ，求 $\text{[math]}$ 面积的最小值；
3. （3）【问题解决】
  某景点有一个形状为菱形 $\text{[math]}$ 的草坪，如图3， $\text{[math]}$ 米， $\text{[math]}$ ，现欲将该草坪扩建为 $\text{[math]}$ ，使得点E、F分别在 $\text{[math]}$ 、 $\text{[math]}$ 的延长线上，且边 $\text{[math]}$ 经过点D，为了节省成本，要求扩建后的草坪面积（ $\text{[math]}$ 的面积）尽可能小，问 $\text{[math]}$ 的面积是否存在最小值？若存在，求出其最小值；若不存在，请说明理由.
答案解析收藏纠错 + 选题