一、选择题:本大题共10小题,每小题4分,共40分.
-
-
-
-
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
-
6.
(2022·浙江模拟)
过

轴正半轴上一点

作圆

的两条切线,切点分别为

,

,若

,则

的最小值为( )
A . 1
B .  C . 2
D . 3
C . 2
D . 3
-
-
A . 3
B .  C . 4
D .
C . 4
D . 
-
-
10.
(2022·浙江模拟)
已知数列

满足

,

,给出下列三个结论:①不存在

,使得数列

单调递减;②对任意的a,不等式

对所有的

恒成立;③当

时,存在常数

,使得

对所有的

都成立.其中正确的是( )
A . ①②
B . ②③
C . ①③
D . ①②③
二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.
-
11.
(2022·浙江模拟)
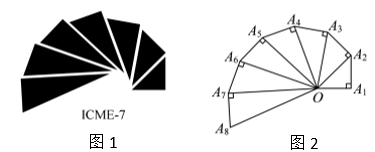
如图1是第七届国际数学教育大会的会徽,它的主题图案是由图2所示的直角三角形演化而成的,设其中的第一个直角三角形

是等腰三角形,且

,它可以形成近似的等角螺线,记

的长度组成数列

,则

=
.
-
12.
(2022·浙江模拟)
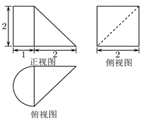
将一个四棱锥和一个半圆柱进行拼接,所得几何体的三视图如右所示,则该几何体的体积为
,表面积为
.
-
-
-
15.
(2022·浙江模拟)
从装有大小完全相同的m个白球,n个红球和3个黑球共6个球的布袋中随机摸取一球,有放回地摸取3次,记摸取的白球个数为X,若

,则m=
,

=
.
-
-
17.
(2022·浙江模拟)
过抛物线

的焦点

作斜率分别为

的两条不同的直线

,且

,

与

相交于点

,

与

相交于点

.分别以

为直径的圆

,圆

(

为圆心)的公共弦记为

,则点

到直线

的距离的最小值为
.
三、解答题:本大题共5小题,共74分.
-
18.
(2022·浙江模拟)
已知函数

.
(Ⅰ)求函数  的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)若函数  关于点
关于点  中心对称,求
中心对称,求  在
在  上的值域.
上的值域.
-
19.
(2022·浙江模拟)
如图,在四棱锥

中,

平面

,

,

,

,

,

为

的中点,点

在棱

上,满足

平面

.
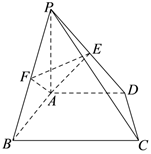
(Ⅰ)求  的值;
的值;
(Ⅱ)求直线  与平面
与平面  夹角的正弦值.
夹角的正弦值.
-
-
21.
(2022·浙江模拟)
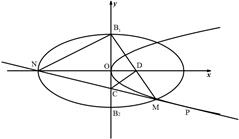
已知椭圆

的上、下顶点分别为

,抛物线


在点

处的切线

交椭圆

于点

,交椭圆的短轴于点

,直线

交

轴于点

.
(Ⅰ)若点  是
是  的中点,求
的中点,求  的值;
的值;
(Ⅱ)设  与
与  的面积分别为
的面积分别为  ,
,  ,求
,求  的最大值.
的最大值.
-
22.
(2022·浙江模拟)
已知函数

.
(Ⅰ)求函数  的最小值;
的最小值;
(Ⅱ)若方程  有两实数解
有两实数解  ,求证:
,求证:  .(其中
.(其中  为自然对数的底数).
为自然对数的底数).
 B .
B .  C .
C .  D .
D . 


和
的通项公式;
满足
,设
的前
项和为
,若实数
满足
对任意的
恒成立,求
的取值范围.

是
的中点,求
的值;
与
的面积分别为
,
,求
的最大值.