B . 
C . 
D . 
B . 
C . 
D . 
B . 开瓶器 
C . 园艺剪刀 
D . 核桃夹子 
B . 
C . 
D . 
B . 
C . 
D . 
B . 
C . 
D . 
①刻度尺测量杆秤上主要刻度的示数 m 到提扭 O 的距离 x，并作出m－x关系图， 如图。
②用刻度尺测量挂钩到的距离 l；
③在 m－x 关系图象中任意读取两组数据 x1、m1 和 x2、m2；
④设杆秤自重 G0 ， 重心到提扭的距离 l0 ， 据杠杆平衡条件，Mgx1=＋G0l0 以及=m2gl＋G0l0 ， 两式可得秤砣质量 M=（用 l、x1、x2、m1、m2 表示）。
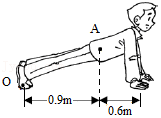
①行李车 
②晾衣竹竿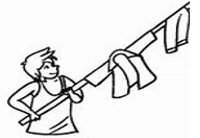 
③做俯卧撑 
④弯腰取物 
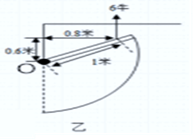
实验1：在直杠杆水平平衡时(如图甲所示)进行实验，记录多组数据。得出：F1×s1＝F2×s2(注：s1和s2分别表示支点到F1和F2的作用点的距离)。在直杠杆倾斜平衡时(如图乙所示)进行实验，也得到了同样的结论。
该结论适用于所有平衡时的杠杆吗？
实验2：科学研究小组用一侧弯曲的杠杆进行如图丙所示的实验，移动钩码，改变钩码数量，记录数据如表，分析表格数据发现上述结论并不成立，但发现一个新的等量关系，即：(待填)。
|
实验次数 |
F1/N |
s1/cm |
F2/N |
s2/cm |
l2/cm |
|
1 |
1.0 |
10.0 |
0.5 |
21.3 |
20.1 |
|
2 |
1.5 |
20.0 |
1.0 |
31.7 |
29.8 |
|
3 |
2.0 |
30.0 |
2.5 |
25.5 |
24.0 |
s和l(支点到力的作用线的距离)这两个量在研究杠杆平衡条件时，哪个量才是有价值的呢？研究小组的同学观察到：支点到F的作用点的距离(s1)与支点到F1的作用线的距离(l1)是相等的。研究小组的同学又进行了实验。
实验3：①移动钩码，使杠杆 (待填) 。
②继续实验，使杠杆平衡，记录F1、s1、l1和F2、s2、l2。
③改变钩码数量，移动钩码，记录杠杆处于平衡时的多组F1、s1、l1和F2、s2、l2。
④分析实验数据，得出弯杠杆的平衡条件。
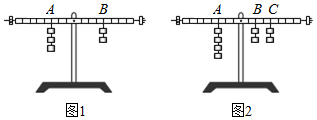
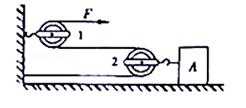
最后，通过科学思维，得出所有杠杆的平衡条件都是：F1×l1＝F2×l2。杠杆的平衡条件可用于解释许多杠杆应用，如用图1方式提升物体比用图2方式省力，就可用杠杆的平衡条件作出合理解释。请回答：
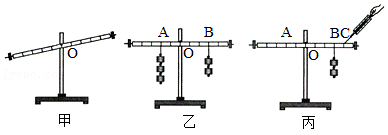
⑴实验前，将杠杆中点置于支架上，杠杆处于水平静止状态。
⑵某同学用如图乙装置通过多次实验操作及数据分析出杠杆平衡的条件是：动力×动力作用点到支点的距离＝阻力×阻力作用点到支点的距离，你认为他的结论（选填：“可靠”或“不可靠”）；
⑶如图乙所示，杠杆在水平位置平衡，若将A、B两点下方挂的钩码同时朝远离支点O方向移动一小格，则杠杆。（选填仍保持平衡/左端下沉/右端下沉）；
⑷取下A点下方所挂钩码，改用弹簧测力计在C点竖直（选填：“向上”或“向下”）拉杠杆，才能使杠杆在水平位置平衡，此时弹簧测力计的示数为F1 ， 如果将弹簧测力计沿如图丙所示方向拉杠杆，使杠杆仍处于水平位置平衡，此时弹簧测力计的示数为F2 ， 则F2F1（选填：“＞”“＝”或“＜”）。
|
次数 |
动力F1/N |
动力臂L1/m |
|
1 |
0.75 |
0.40 |
|
2 |
1.0 |
0.30 |
|
3 |
1.5 |
0.20 |
|
4 |
2.00 |
0.15 |
|
5 |
3.0 |
0.10 |
