天津市滨海新区2021-2022学年七年级下学期期末数学试题

更新时间：2022-08-09 浏览次数：154 类型：期末考试

一、单选题

1. (2024七下·田阳期末) 9的平方根是（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 9

答案解析收藏纠错 + 选题
2. (2022七下·滨海期末) 若点 $\text{[math]}$ 在y轴上，则点P的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022七下·滨海期末) 估计 $\text{[math]}$ +1的值在（）

A . 1到2之间 B . 2到3之间 C . 3到4之间 D . 4到5之间

答案解析收藏纠错 + 选题
4. (2022七下·滨海期末) 在实数 $\text{[math]}$ 中，有理数的个数为（）

A . 3个 B . 4个 C . 5个 D . 6个

答案解析收藏纠错 + 选题
5. (2022七下·滨海期末) 下列说法正确的是（）

A . 16的平方根是 $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ =±4 D . 以上都不对

答案解析收藏纠错 + 选题
6. (2022七下·滨海期末) 如图，设点P是直线l外一点， $\text{[math]}$ ，垂足为点Q，点T是直线l上的一个动点，连接 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·恩施期中) 下列图形中，由∠1=∠2能得到AB∥CD的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2022七下·滨海期末) 下列调查中，最适合采用全面调查的是（）

A . 了解我市中学生的消防安全意识 B . 了解我市中学生每周体育锻炼的时间 C . 了解某品牌新能源车的行驶里程 D . 对我国首艘国产航母各种零部件质量情况的调查

答案解析收藏纠错 + 选题
9. (2023七下·定兴期末) 若 $\text{[math]}$ ，则下列不等式一定成立的是：（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022七下·滨海期末) 下列说法错误的是（）

A . 对顶角相等 B . 两点之间，线段最短 C . 同旁内角相等 D . 若a∥b且b∥c，则a∥c

答案解析收藏纠错 + 选题
11. (2022八上·成都期末) 《九章算术》是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响.该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元.问有多少人?该物品价几何?设有x人.物品价值y元，则列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2022七下·滨海期末) 关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 的解集为 $\text{[math]}$ ，那么 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

13. (2022七下·滨海期末) $\text{[math]}$ 的相反数是， $\text{[math]}$ 的绝对值是．

答案解析收藏纠错 + 选题
14. (2022七下·滨海期末) 如图，直线AB、CD、EF相交于点O，则∠1+∠2+∠3＝°．

答案解析收藏纠错 + 选题
15. (2024七下·天津市期末) 一个容量为80的样本最大值是123，最小值是50，用频数分布直方图描述这一组数据，取组距为10，则可以分成组．

答案解析收藏纠错 + 选题
16. (2022七下·海伦期末) 已知点M坐标为 $\text{[math]}$ 且M点到两坐标轴的距离相等，则点的M坐标是．

答案解析收藏纠错 + 选题
17. (2023七下·东莞期中) 若关于x，y的方程组 $\text{[math]}$ 的解x与y相等，则k的值为．

答案解析收藏纠错 + 选题

三、解答题

18. (2022七下·滨海期末) 李强同学学完“相交线与平行线”一章后，在一本数学读物上看到一种只利用圆规和无刻度直尺作图的方法：
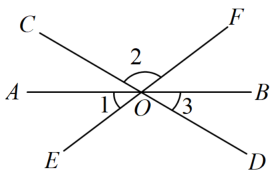
① 以∠AOB的顶点O为圆心，以适当长为半径画弧，交OA边于点M，交OB边于点N；② 作一条射线CD，以点C为圆心，以OM长为半径画弧，与射线CD交于点E；③ 以点E为圆心，以MN长为半径画弧，与②中所画弧交于点F；④ 过点F作射线CP，则∠PCD=∠BOA．如图1：
李强想利用这种方法过平面内一点Q作直线l的平行线a，如图2．
1. （1）李强同学能借助上述方法作出直线l的平行线a吗？（填“能”或“不能”）.
2. （2）如果能，请在图2中作出直线a，保留作图痕迹，并说明能够证明这两条直线平行的理由： ▲ ．
答案解析收藏纠错 + 选题
19. (2022七下·滨海期末) 推理填空：完成下面的证明过程．
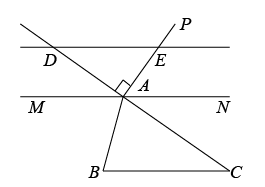
如图，AD $\text{[math]}$ EF，∠1+∠2＝180°，DG⊥AC于点G，∠BAC＝90°．
求证：DG平分∠ADC．
证明：∵DG⊥AC（已知），
∴∠DGC＝90°（   ）．
∵∠BAC＝90°（已知），
∴∠DGC＝∠BAC，
∴  ▲   $\text{[math]}$ AB（  ），
∴∠BAD＝∠ADG （   ）．
∵AD $\text{[math]}$ EF（已知），
∴∠BAD+  ▲  ＝  ▲  （    ）．
∵∠1+∠2＝180°（已知），
∴∠BAD＝  ▲  （等量代换），
∴∠ADG＝  ▲  （等量代换），
∴DG平分∠ADC （    ）．

答案解析收藏纠错 + 选题
20. (2022七下·滨海期末) 解方程组：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
21. (2022七下·滨海期末) 解不等式组 $\text{[math]}$
请结合题意填空，完成本题的解答．
1. （1）解不等式①，得；
2. （2）解不等式②，得；
3. （3）把不等式①和②的解集在数轴上表示出来：
4. （4）原不等式组．
答案解析收藏纠错 + 选题
22. (2022七下·滨海期末) 某同学在学习了数据的收集、整理与描述后，对其居住区域的部分居民随机进行了“手机品牌忠诚度”的问卷调查：A代表华为手机，B代表小米手机，C代表OPPO手机，D代表苹果手机，E代表VIVO手机，F代表其他品牌手机，并根据调查结果绘制成如图两幅不完整的统计图：
解答下列问题：
1. （1）由图可知，有人参与了本次调查；
2. （2）扇形统计图中，m的值是；
3. （3）根据以上信息直接在答题卡中补全条形统计图；
4. （4）根据以上调查结果，如果某同学所在的小区有6000人，请你估计该小区信赖华为手机的人数．
答案解析收藏纠错 + 选题
23. (2022七下·滨海期末) 如图，点D是三角形ABC边CA延长线上一点，过点A作DC的垂线AP，MN是过点A的一条直线，且∠MAB=∠B，过点D作DE∥MN交AP于点E，求证：∠C+∠DEA=90°．

答案解析收藏纠错 + 选题
24. (2022七下·滨海期末) 某地面对形势异常严峻的新冠疫情，遵从党和国家部署，最大程度保障人民群众的健康，将所在区域划分为封控区、管控区和防范区. 现要将一批蔬菜运往封控区，已知用3辆A型车和1辆B型车装满蔬菜一次可运26吨；用1辆A型车和2辆B型车装满蔬菜一次可运22吨．
1. （1）求一辆A型车和一辆B型车装满蔬菜分别可运多少吨？
2. （2）若一辆A型车的租金是180元，一辆B型车的租金是220元，该地计划租用A型车和B型车共7辆，且租金不超过1400元，问最多可租用几辆B型车？
答案解析收藏纠错 + 选题
25. (2022七下·滨海期末) 如图，三角形AOB在平面直角坐标系中，A，B两点的坐标分别为（2 ， 4），（6 ， 2），O是坐标原点．
1. （1）如图1，若把三角形AOB向左平移2个单位长度，然后再向上平移1个单位长度，顶点A、O、B的对应点分别是A′、O′、B′，则A′、O′、B′三个点的坐标分别是多少？
2. （2）求三角形AOB的面积；
3. （3）如图2，x轴上一动点P，从点（－3 ， 0）运动到点（2 ， 0），连接PA和PB，求三角形APB面积的取值范围．
答案解析收藏纠错 + 选题