一、选择题(本大题共12小题,每小题2分,共24分.)
-
A . 2个
B . 3个
C . 4个
D . 5个
-
-
A . x=2
B . x≥2
C . x>﹣2
D . x>2
-
4.
(2022八下·凉山期末)
一次函数y=mx+n与y=mnx(m,n为常数,且mn≠0),在同一平面直角坐标系的图像是( )
-
A . 3,5,9
B . 4,6,8
C .  D .
D . 
-
A . 平均数
B . 众数
C . 中位数
D . 方差
-
-
A . 16
B . 25
C . 144
D . 169
-
9.
(2022八下·凉山期末)
在平行四边形ABCD中,AC、BD相交于O,AC=10,BD=8,则AD的长度的取值范围是( )

A . AD>1
B . 1<AD<9
C . AD<9
D . AD>9
-
10.
(2022八下·凉山期末)
如图,在正方形ABCD中,AB=6,点Q是AB边上的一个动点(点Q不与点B重合),点M,N分别是DQ,BQ的中点,则线段MN的长度为( )

A .  B .
B .  C . 3
D . 6
C . 3
D . 6
-
11.
(2022八下·凉山期末)
若△ABC的三边a,b,c满足a
2+b
2+c
2+338=10a+24b+26c,则ABC的面积是( )
A . 338
B . 24
C . 26
D . 30
-
12.
(2022八下·凉山期末)
如图,矩形ABCD的面积为20cm
2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC
1B,对角线交于点O
1;以AB、AO
1为邻边作平行四边形AO
1C
2B⋯⋯依此类推,则平行四边形AO
4C
5B的面积为( )

二、填空题(本大题共8小题,每小题3分,共24分)
-
-
-
-
16.
(2022八下·凉山期末)
甲、乙、丙三人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,方差分别是:S
甲2=0.90,S
乙2=1.22,S
丙2=0.43,则在本次射击测试中,成绩最稳定的是
.
-
17.
(2022八下·凉山期末)
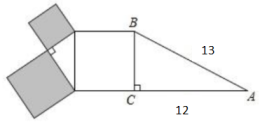
如图,沿折痕AE折叠矩形ABCD的一边,使点D落在BC边上一点F处,若AB=8,且△ABF的面积为24,则EC的长为
.

-
-
19.
(2022八下·凉山期末)
如图,圆柱形玻璃杯,高为12cm,底面周长为10cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为
(玻璃杯厚度忽略不计).

-
三、解答题(本大题共7个小题,共52分.解答过程应写出必要的文字说明和解答少G,
-
-
(1)
计算:

|

2|;
-
(2)
已知x=1

, 求x
2+y
2﹣xy﹣2x+2y的值.
-
22.
(2022八下·凉山期末)
某校八年级举行了主题为“珍惜海洋资源”的知识竞赛活动,为了了解全年级500名学生此次参加竞赛的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图.
|
组别
|
分数(分)
|
频数
|
|
A
|
60≤x<70
|
a
|
|
B
|
70≤x<80
|
10
|
|
C
|
80≤x<90
|
14
|
|
D
|
90≤x<100
|
18
|

-
-
(2)
所抽取的参赛学生成绩的中位数落在哪个组别?
-
(3)
估计该校八年级竞赛成绩达到80分及以上的学生有多少人?
-
-
-
(2)
若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
-
-
(1)
若梯子底端离墙角的距离OB为0.7米,求这个梯子的顶端A距地面有多高?
-
(2)
在(1)的条件下,如果梯子的顶端A下滑0.4米到点A,那么梯子的底端B在水平方向滑动的距离BB为多少米?
-
-
-
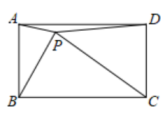
(2)
如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.
-
26.
(2022八下·凉山期末)
阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1 , y1)、P2(x2 , y2),其两点间的距离 , 同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1||或|y2﹣y1|.
, 同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1||或|y2﹣y1|.
-
(1)
已知A(3,4)、B(﹣2,﹣8),试求A、B两点间的距离;
-
(2)
已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;
-
(3)
已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.
-
27.
(2022八下·凉山期末)
在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(4,8),点A的坐标为(28,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒

-
-
(2)
当t为何值时,四边形OEDC是平行四边形?
-
(3)
连接AD,记△ADE的面积为S,求S与t的函数关系式.
 B .
B . 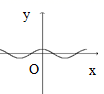 C .
C .  D .
D . 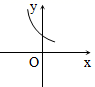
 B .
B .  C .
C .  D .
D . 










, 同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1||或|y2﹣y1|.
