一、选择题(共8小题,每小题3分,计24分。每小题只有一个选项是符合题意的)
-
A . m≠0
B . m≠3
C . m=0
D . m=3
-
A . (x+1)2=2
B . (x﹣1)2=2
C . (x+1)2=0
D . (x﹣1)2=0
-
3.
(2022九上·榆林月考)
如图,在菱形ABCD中,对角线AC、BD交于点O,已知AO=2,OB=4,则菱形ABCD的面积是( )

A . 4
B . 8
C . 16
D . 20
-
-
A . 2
B . ﹣2
C . 4
D . ﹣4
-
A . AC=BC=CD=DA
B . AO=BO=CO=DO,AC⊥BD
C . AO=CO,BO=DO,AC⊥BD
D . AB=BC,CD⊥DA
-
7.
(2023九上·江油期中)
我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )
A . 3(x﹣1)x=6210
B . 3(x﹣1)=6210
C . (3x﹣1)x=6210
D . 3x=6210
-
8.
(2022九上·榆林月考)
如图,在矩形ABCD中,O为AC的中点,过点O的直线分别与BC,AD交于点E,F,连接BO,CF.若AB=BO,BE=EO,则下列结论中错误的是( )

A . AC⊥EF
B . EF=FC
C . BE+DF=EF
D . AD=2AB
二、填空题(共5小题,每小题3分,计15分)
-
-
-
-
12.
(2022九上·榆林月考)
“新冠肺炎”防治取得战略性成果,若有一个人患了“新冠肺炎”,经过两轮传染后共有25个人患了“新冠肺炎”,则每轮传染中平均一个人传染了
人.
-
13.
(2022九上·榆林月考)
如图,正方形ABCD和正方形BEFG,点F,B,C在同一直线上,连接DF,M是DF的中点,连接AM,若BC=4,AM=

, 则正方形BEFG的边长为
.

三、解答题(共13小题,计81分。解答应写出过程)
-
-
-
16.
(2022九上·榆林月考)
如图,在Rt△ABC中,∠ACB=90°,D为AB中点,BE∥CD,CE∥AB.试判断四边形BDCE的形状,并证明你的结论.

-
17.
(2022九上·榆林月考)
已知关于x的一元二次方程2x
2+2mx+m﹣1=0,求证:不论m取什么实数,这个方程总有两个不相等的实数根.
-
18.
(2023·章丘模拟)
如图,在菱形ABCD中,M,N分别是AB和BC上的点,且AM=CN,求证:∠DMN=∠DNM.

-
19.
(2022九上·榆林月考)
已知一元二次方程x
2+2x﹣m=0有两个不相等的实数根x
1 , x
2 , 若x
1•x
2﹣(x
1+x
2)=﹣3,求m的值.
-
20.
(2022九上·榆林月考)
如图,点A在∠MON的边ON上,AB⊥OM于点B,AE=OB,DE⊥ON于点E,AD=AO,DC⊥OM于点C,求证:四边形ABCD是矩形.

-
21.
(2022九上·榆林月考)
新能源汽车节能、环保,越来越受消费者喜爱.2020年某款新能源汽车销售量为15万辆,销售量逐年增加,2022年预估当年销售量为21.6万辆,求这款新能源汽车销售量的年平均增长率.
-
22.
(2022九上·榆林月考)
如图,在正方形ABCD中,E是BD上一点,F是CD上一点,连接EF,给出下列三条
信息:①BE=AB,②DE=CF,③EF⊥BD.
请从上述三条信息中选择两个作为已知条件,选择另外一个作为结论,并写出结论成立的证明过程.
你选择的条件是 , 结论是 . (填序号)

-
23.
(2022九上·汉阴月考)
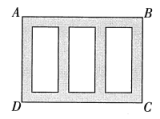
如图,矩形

是某会展中心一楼展区的平面示意图,其中边

的长为40米,边

的长为25米,该展区内有三个全等的矩形展位,每个展位的面积都为200平方米,阴影部分为宽度相等的人行通道,求人行通道的宽度.
-
-
25.
(2022九上·榆林月考)
某商场销售一批名牌衬衫,每件进价为100元,若每件售价为160元,则平均每个月可售出100件,经调查发现,每件衬衫每降价2元,商场平均每月可多售出10件,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,设每件衬衫降价x元.
-
(1)
用含x的代数式表示每月可售出的衬衫件数为件;
-
(2)
若商场销售这种衬衫每月要盈利7875元,请你帮助商场算一算,每件衬衫应降价多少元?
-
26.
(2022九上·榆林月考)
如图1,已知在▱ABCD中,BE平分∠ABC,交AD于点E,过点E作EF∥AB,交BC于点F,O是BE的中点,连接OF,OC,OD.

-
-
(2)
若∠ABC=90°,如图2所示:
①求证:∠ADO=∠BCO;
②若∠EOD=15°,AE=1,求OC的长.









