北京市顺义区2021-2022学年八年级下学期期末数学试题

更新时间：2024-07-13 浏览次数：104 类型：期末考试

一、单选题

1. (2022八下·顺义期末) 下列图案中，不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2022八下·顺义期末) 方程 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2022八下·顺义期末) 点 $\text{[math]}$ 关于x轴对称的点P’的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八下·青山期末) 某校组织环保知识竞赛，为参加区级比赛做选手选拔工作，经过多次测试后，有4名同学成为区级参赛选手的候选人，具体情况如下表：

甲
乙
丙
丁
平均分
90
92
95
95
方差
36
32
21
33
如果从这4名同学中选出1位参加区级比赛（总体水平高且状态稳定），你会推荐（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
5. (2022八下·顺义期末) 一元二次方程 $\text{[math]}$ 配方后可化为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022八下·顺义期末) 如果一组数据 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 的平均数为 $\text{[math]}$ ，方差为 $\text{[math]}$ ，则数据 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ 的平均数和方差分别是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022八下·顺义期末) 学习了四边形之后，王老师用如下图所示的方式表示了四边形与特殊的四边形的关系，则图中的“M”和“N”分别表示（）

A . M表示菱形，N表示正方形 B . M表示正方形，N表示菱形 C . M表示正方形，N表示梯形 D . M表示菱形，N表示梯形

答案解析收藏纠错 + 选题
8. (2022八下·顺义期末) 如图，在平面直角坐标系xOy中，点A的坐标是（3， 0），点B是函数 $\text{[math]}$ (0<x＜4)的图像上的一个动点，过点B作BC⊥y轴交函数 $\text{[math]}$ 的图像于点C，点D在x轴上（点D在点A的左侧），且AD=BC，连接AB，CD．有如下四个结论：
①四边形ABCD一定是平行四边形；②四边形ABCD可能是菱形；③四边形ABCD可能是矩形；④四边形ABCD可能是正方形．所有正确结论的序号是（）

A . ①②③ B . ②③④ C . ①③④ D . ①②④

答案解析收藏纠错 + 选题

二、填空题

9. (2022八下·顺义期末) 函数 $\text{[math]}$ 中，自变量 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
10. (2022八下·顺义期末) 如图，在 $\text{[math]}$ 中，点D，E分别是AB，BC的中点，若AC=6，则DE的长为．

答案解析收藏纠错 + 选题
11. (2022八下·顺义期末) 某校对520名女生的身高进行了测量，身高在1.55~1.60（单位：m）这一小组的频率为0.3，则该小组有人．

答案解析收藏纠错 + 选题
12. (2022八下·顺义期末) 如图所示的多边形中，根据标出的各内角度数，求出x的值是．

答案解析收藏纠错 + 选题
13. (2022八下·顺义期末) 若关于x的方程 $\text{[math]}$ 的一个根是-1，则m的值是．

答案解析收藏纠错 + 选题
14. (2022八下·顺义期末) 已知，一次函数 $\text{[math]}$ 的图象如图所示，那么k0，b0 （填“＜”，“＞”或“=”）．

答案解析收藏纠错 + 选题
15. (2022八下·顺义期末) 已知关于x的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则k＝．

答案解析收藏纠错 + 选题
16. (2022八下·顺义期末) 等边△ABC的边长为4，点D是BC边上的任意一点（不与点B，C 重合），过点D分别作 $\text{[math]}$ ， $\text{[math]}$ ，交AB，AC于点E，F，则四边形AEDF的周长是．

答案解析收藏纠错 + 选题

三、解答题

17. (2022八下·顺义期末) 一次函数y =kx+b（ $\text{[math]}$ ）的图像经过点 $\text{[math]}$ ， $\text{[math]}$ ，求一次函数的表达式．

答案解析收藏纠错 + 选题
18. (2022八下·顺义期末) 如图，四边形 $\text{[math]}$ 和 $\text{[math]}$ 都是平行四边形.求证：四边形 $\text{[math]}$ 是平行四边形.

答案解析收藏纠错 + 选题
19. (2024九上·白云期中) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
20. (2022八下·顺义期末) 已知：如图，菱形ABCD中，对角线AC，BD交于点O， $\text{[math]}$ ．
1. （1）求证：四边形AODE是矩形；
2. （2）若AB=8，∠ABC=60°，求矩形AODE的周长．
答案解析收藏纠错 + 选题
21. (2022八下·顺义期末) 2022年北京冬奥会的举办促进了冰雪旅游，小明为了解寒假期间冰雪旅游的消费情况，从某滑雪场的游客中随机抽取了50人，获得了这些游客当天消费额（单位：元）的数据，并对数据进行整理、描述和分析．下面给出部分信息：
a．滑雪场游客消费额数据的频数分布直方图如下（数据分成6组：0≤x＜200，200≤x＜400，400≤x＜600，600≤x＜800，800≤x＜1000，1000≤x＜1200）：
b．滑雪场游客消费额数据在400≤x＜600这一组的是：410 430 430 440 440 440 450 450 520 540
c．滑雪场游客消费额数据的平均数为420元．
根据以上信息，解决下列问题：
1. （1）求滑雪场游客消费额数据在600≤x＜800这一组的频率，并补全频数分布直方图；
2. （2）滑雪场游客消费额数据的中位数是；
3. （3）若滑雪场在寒假期间的一个月内日均游客人数为300人，估计滑雪场这个月（按30天计算）的游客消费总额．
答案解析收藏纠错 + 选题
22. (2022八下·顺义期末) 列方程解应用题：某工厂一月份的产品产量为 100 万件，由于工厂管理理念更新，管理水平提高，产量逐月提高，三月份的产量提高到144万件，求一至三月该工厂产量的月平均增长率．

答案解析收藏纠错 + 选题
23. (2022八下·顺义期末) 已知：直线l和l外一点A．求作：l的平行线，使它经过点A．
作法：①在直线l上任取一点B，以点B为圆心，任意长为半径作弧，交直线l于点C；②连接AB，分别以点A，C为圆心，以BC，AB的长为半径作弧，两弧相交于点D（点D在l的上方）；③作直线AD．所以直线AD即为所求．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；
2. （2）完成下面的证明．
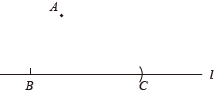
  证明：连接CD．
  ∵ AD=BC，DC=AB，
  ∴四边形ABCD是 ▲ ，（）（填推理依据）．
  ∴ $\text{[math]}$ （）（填推理依据）．
  即 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
24. (2022八下·顺义期末) 已知：关于x的方程 $\text{[math]}$ ．
1. （1）请判断这个方程根的情况；
2. （2）若该方程的一个根小于1，求k的取值范围．
答案解析收藏纠错 + 选题
25. (2022八下·顺义期末) 已知一次函数 $\text{[math]}$ 的图像与正比例函数 $\text{[math]}$ （k≠0）的图像交于点A．
1. （1）当点A的坐标为（2，1）时．
  ①求m，k的值；
  ②当 $\text{[math]}$ 时， $\text{[math]}$ ▲ $\text{[math]}$ （填“>”，“=”或“<”）．
2. （2）当m >0时，若交点A在第三象限，结合图像，直接写出k的取值范围．
答案解析收藏纠错 + 选题
26. (2022八下·顺义期末) 在平面直角坐标系xOy中，已知点A（-2，2），点B（-3，-2）．
1. （1）如果四边形ABCD是以原点O为对称中心的平行四边形，直接写出点C、D的坐标；
2. （2）记横、纵坐标都为整数的点叫做整点．
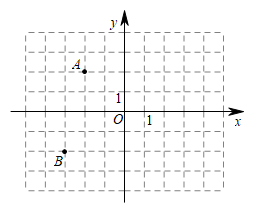
  ①写出（1）中的平行四边形ABCD内部（不包括边界）的整点的个数；
  ②已知平行四边形 $\text{[math]}$ 的对称中心在x轴上，且点M，点N分别在点B，A的右侧，当平行四边形 $\text{[math]}$ 内部（不包括边界）的整点的个数恰好为9个时，设直线MN的表达式为y=kx+b，求k的值及b的取值范围．
答案解析收藏纠错 + 选题
27. (2022八下·顺义期末) 如图，AC是正方形ABCD的对角线，点P在AC上，点E在边AD上，作∠EPF＝90°，PF与射线AB交于点F．
1. （1）依题意补全图形；
2. （2）用等式表示线段PE与PF之间的数量关系，并证明；
3. （3）直接写出线段AE，AP和AF之间的数量关系．
答案解析收藏纠错 + 选题
28. (2022八下·顺义期末) 在平面直角坐标系xOy中，对于点 $\text{[math]}$ ，给出如下定义：当点 $\text{[math]}$ 满足 $\text{[math]}$ 时，称点 $\text{[math]}$ 是点 $\text{[math]}$ 的等积点．已知，点 $\text{[math]}$ ．
1. （1）在 $\text{[math]}$ （2，4）， $\text{[math]}$ （-1，-2）， $\text{[math]}$ （0，1）中，点 $\text{[math]}$ 的等积点是；
2. （2）若点A（t，t ²）是点P的等积点，求t 的值；
3. （3）点B在直线 $\text{[math]}$ 上，若点P的等积点（原点除外）也是点B的等积点，求点B的坐标．
答案解析收藏纠错 + 选题